슈퍼짱짱

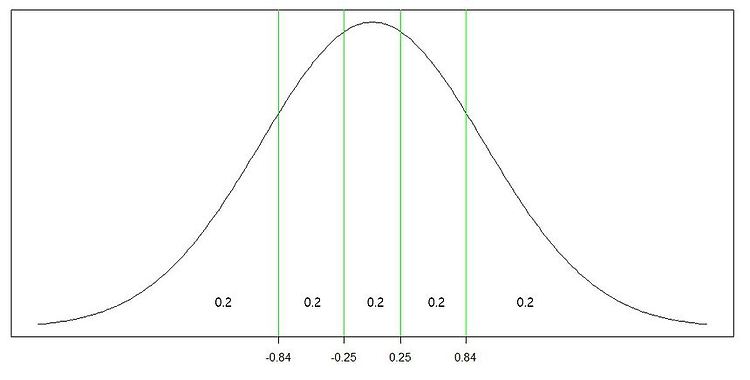
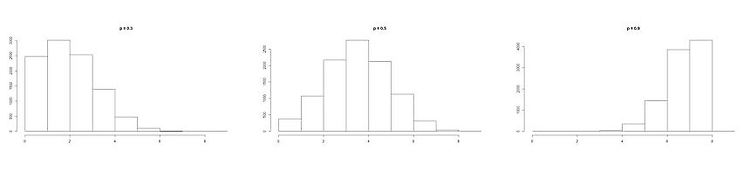
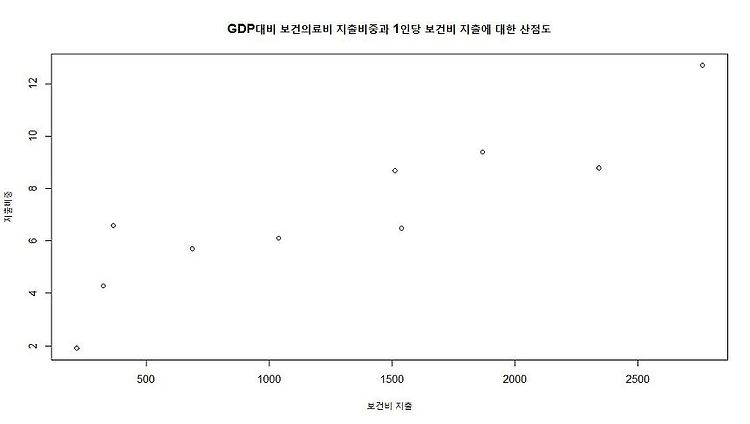
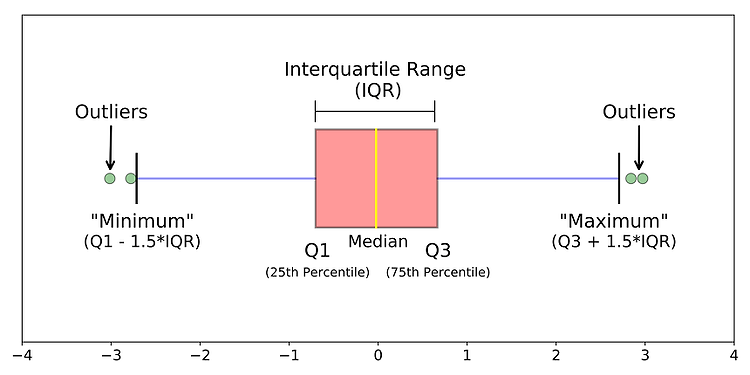
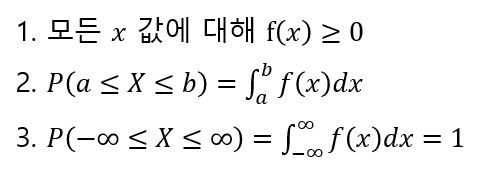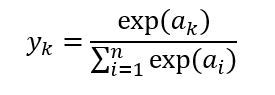이전에 셀 수 있는 값들의 분포인 베르누이, 이항분포에 대해 알아보았다.이번에는 확률변수가 취하는 값들이 셀 수 있는 것이 아니라 시간, 몸무게, 0과 1사이의 임의의 실수처럼 셀 수 없는 연속적인 값을 가지는 연속확률분포들 중에서 대부분의 통계학 이론의 기본이 되는 정규분포에 관하여 알아보자. 연속확률분포란? 정규분포를 알아보기에 앞서, 연속확률분포에 대해 알아보자. 연속확률변수 X는 주어진 구간의 모든 값을 가질 수 있으므로, 앞서 배운 이산확률분포와는 다른 방식으로 표현해야 한다. 예를 들어, X~Bin(5, 0.25) 에서 P(X=4) = 5C4*(0.25)^4*(0.75)^1 = 0.015 이다. 그렇다면 X가 연속적인 값을 가질 수 있는 상황에서 X=4일 확률은 무엇일까? 신생아의 몸무게가 3..

정규확률그림이란? What is Q-Q plot? 많은 경우에 통계적인 절차나 분석 등에서 모집단의 분포가 정규분포를 따른 다는 가정을 하고 있다. 그렇다면 표본을 추출했을 때 이러한 정규모집단의 가정을 조사하는 방법은 어떤 것이 있을까? 그 방법 중 하나가 바로 정규확률그림으로 확인하는 것이다.정규점수그림(normal scores plot) 또는 정규확률그림(normal probability plot)이라 하는데 정규확률그림이라는 용어를 더 많이 쓴다. 이 때, 정규점수(normal scores)란 표준정규분포(mean=0,sd=1)에서의 이상적인 표본을 말한다. 즉, 표준정규분포의 확률밀도함수를 등확률 구간으로 나누어 주는 경계값(z값)을 의미한다. 분위수를 생각해보면 쉽다. n분위수에 해당하는 z값..

이전 포스팅에서 베르누이 시행에 대해 알아보았다. 본 포스팅에서는 이항분포에 대해 알아보겠다. 이항분포란? 성공할 확률이 p인 베르누이 시행을 n번 반복할 때에 일어나는 성공의 횟수를 X라 하면, 이 확률변수 X의 확률변수를 모수가 (n, p)인 이항분포라 한다. 즉, 쉽게 생각해 경우의 수가 2개뿐인 실험 1번 시행 - 베르누이/ 베르누이를 n번 시행 - 이항분포 이항분포(binomial distribution) n : 베르누이 시행의 반복 횟수 p : 각 시행에서 성공할 확률, P(S)X : n번 시행 중 성공의 횟수 이와 같이 정의된 확률변수 X를 이항 확률변수라 하고 그 분포를 이항분포라 한다. X~Bin(n,p)로 표현하기도 한다. 이항 확률변수 X가 취하는 값의 범위는 0, 1, 2, ...,..

기초통계 - 이항분포와 관련있는 베르누이 두 그룹으로 나누어져 있는 모집안에서 표본을 추출하는 경우, 각 단계의 추출은 두 가지의 결론만을 갖게된다. 동전던지기가 그 예이다. 동전을 던졌을 때 그 결과는 앞면, 뒷면으로 두 가지만 나타난다. 이런 경우 매번 반복되는 추출(실험)을 통계학용어로 시행(trial)이라 부르고, 두 개의 가능한 결과 중 하나는 성공(S, success), 다른 하나는 실패(F, failure)라 부르는데, 이는 시행 결과가 두 개뿐임을 의미하며 진짜 성공과 실패와는 부관하다. 보통 관심있는 결과를 성공이라 부른다. 이 '성공'과 '실패'로 나타나는 시행이 반복되면서 다음과 같은 조건이 만족되는 경우 이를 베르누이 시행이라 부른다. 베르누이 시행(Bernoulli trial) (..

상관계수란? 이전 포스팅에서 두 연속형 변수의 관계를 눈으로 확인하기 위한 산점도에 대해 알아보았다.산점도로부터 파악할 수 있는 관계는 객관성이 부족한 면이 있다. 예를 들어 동일한 크기의 좌표평면에서 좌표의 눈금을 변화시키면(변수의 측정 단위를 변화시키면) 두 변수의 관계가 다른 것처럼 보여질 수 있다. 따라서 좀 더 객관적으로 두 변수간의 관계를 알아볼 수 있는 상관계수에 대해 알아보겠다. 두 변수로 산점도를 그려보면 직선, 곡선 등 여러 형태를 가질 수 있는데, 여기서 가장 관심이 있는 경우는 직선의 형태이다. 산점도에서 점들이 얼마나 직선에 가까운가의 정도를 나타내는데 쓰이는 측도가 상관계수이다. 상관계수란? 두 변수 x,y 사이의 상관관계의 정도를 나타내는 수치 상관계수는 피어슨(Karl Pea..

두 연속형 변수의 요약 : 산점도 지난 포스팅에서 두 범주형 변수의 요약방법인 분할표에 대해 알아보았다.이번에는 두 연속형 변수의 관계를 알아보기 위한 첫 번째 단계인 산점도에 대해 알아보겠다. 두 연속형 변수 x와 y에 대해 1. 두 변수는 서로 관계가 있는가? 2. 있다면, 어떤 관계인가? 라는 질문을 할 수 있다.이 때, (x,y)에 대해 그림을 그려 그 관계를 눈으로 파악 할 수 있는데, 이 그림을 산점도라 한다. 산점도란? 변수 x를 수평축에 놓고 변수 y를 수직축에 놓은 후에 각 관측값의 짝을 좌표 위에 표시함으로써 얻게되는 그림 이렇게 그린 그림을 관측값들이 직선이나 곡선의 띠를 형성하고 있는지, 또는 특별한 경향 없이 무작위로 흩어져있는지 확인할 수 있다. 예)1990년도 국가별 국내총생산..

두 범주형 변수의 요약 : 분할표 분할표란? 두 변수에 대한 관측값을 요약하고 해석하는 방법 중 하나로, 두 변수가 모두 범주형에 속할 때, 도수분포표를 2차원으로 확장한 형태로 요약할 수 있다.한 변수에 대한 범주는 왼쪽에, 또 다른 변수에 대한 범주는 위쪽에 표시하고, 두 변수의 범주들이 교차하는 칸마다 각 변수의 범주를 동시에 갖는 관측값들의 수를 그 칸의 도수로 기록한다. 이렇게 도표로 요약된 자료를 분할표라 부른다. >>> 범주형자료란? 바로가기>>> 범주형자료 표현하는 방법 바로가기 예)새로이 제한된 어떤 정책에 대한 지지여부를 알아보기 위하여 400명을 임의로 추출하여 조사했다.표본으로 추출된 각 개인의 성별과 지지여부를 해당 범주에 따라 정리한 결과가 다음과 같다.  찬성 미결정 반대 합계..

소프트맥스란? What is softmax? softmax란? 신경망의 출력층에서 사용하는 활성화 함수로, 분류문제에 쓰이는 함수이다. * 회귀에서는 항등함수(identity function)을 사용한다. softmax의 식은 다음과 같다. 파이썬에서 소프트맥스 함수 구현하기 (softmax in python) 파이썬에서 seoftmax 함수는 다음과 같이 구현한다. 12345678import numpy as np def softmax(a) : exp_a = np.exp(a) sum_exp_a = np.sum(exp_a) y = exp_a / sum_exp_a return ycs 이를 한 줄씩 실행하면 다음과 같다. 1234a = np.array([0.3,2.9,4.0])exp_a = np.exp(a)s..

앞서 리뷰했던 중심의 위치, 퍼진 정도 등의 수치들은 자료의 여러 성질을 나타내지만, 자료 전체의 대략적인 모양을 보여 주지는 못하는 단점이 있다. >> 평균 vs 중앙값 vs 최빈값 바로가기>> 분산 & 표준편차란? 바로가기 >> 백분위수 & 사분위수란? 바로가기 이에 이번 포스팅에서는 상자그림에 대해 알아보고 R에서 직접 구현하는 방법도 알아보겠다. 상자그림이란? 상자그림(boxplot)이란? 자료로부터 얻는 다섯 가지 요약수치인 최소값, Q1, Q2, Q3, 최대값을 가지고 그림을 그린것이다. box plot을 그리는 자세한 과정은 다음과 같다. 1. 사분위수(Q1, Q2, Q3)를 결정한다. 2. Q1과 Q3을 네모난 상자로 연결하고, 중앙값(Q2)의 위치에 수직선을 긋는다.3. IQR = Q3 ..

EXPLAINING AND HARNESSING ADVERSARIAL EXAMPLES 논문 리뷰 위와 같이 판다를 판다라고 잘 인식하는 network에 어떠한 noise를 섞어 높은 확률로 다른 class로 인식하게 하는 것을 ADVERSARIAL Attack 이라 한다. 그리고 이 때, 노이즈가 포함된 이미지 즉, 위에서 가장 오른쪽 사진들을 ADVERSARIAL EXAMPLES 라 한다. 단, 노이즈가 포함된 사진도 사람이 보기에는 원래의 사진과 구분되지 않아야 한다. 그럼 이제 ADVERSARIAL EXAMPLES 을 만드는 기법 중 하나인 FGSM(fast gradient sign method) 에 대해 알아보겠다.* 이 논문은 GAN의 저자로 유명한 Goodfellow에 의해 발표되었다. 하지만,..