EXPLAINING AND HARNESSING ADVERSARIAL EXAMPLES 논문 리뷰
위와 같이 판다를 판다라고 잘 인식하는 network에 어떠한 noise를 섞어 높은 확률로 다른 class로 인식하게 하는 것을 ADVERSARIAL Attack 이라 한다. 그리고 이 때, 노이즈가 포함된 이미지 즉, 위에서 가장 오른쪽 사진들을 ADVERSARIAL EXAMPLES 라 한다. 단, 노이즈가 포함된 사진도 사람이 보기에는 원래의 사진과 구분되지 않아야 한다.
그럼 이제 ADVERSARIAL EXAMPLES 을 만드는 기법 중 하나인 FGSM(fast gradient sign method) 에 대해 알아보겠다.
* 이 논문은 GAN의 저자로 유명한 Goodfellow에 의해 발표되었다. 하지만, GAN과는 전혀 다른 기술이다.
* 본 논문 리뷰에는 매우 주관적인 설명이 많이 들어가니, 틀린 부분이 있다면 알려주시면 감사하겠습니다:)
논문 링크 : https://arxiv.org/pdf/1412.6572.pdf
ABSTRACT
신경망을 포함한 몇몇의 머신러닝 모델들은 adversarial examples을 잘못 분류한다. 작지만 의도적으로 perturbations(작은 변화 - noise를 의미함)를 데이터에 적용함으로써, 교란된 입력으로 인해 모델이 높은 확률로 오답을 출력하도록한다.
초기에는 이를 비선형성과 과적합으로 설명하려 했지만, 우리는 선형성으로 설명하고자 한다.
1. INTRODUCTION
최신의 신경망 모델을 포함하여 몇몇의 머신러닝 모델들은 adversarial examples에 취약하다. 즉, 이 머신러닝 모델들은 잘 분류되는 데이터와 아주 약간 다른 예제들(아주 작은 noise가 포함된 예제들)을 잘못 분류한다. 이것은 adversarial examples이 우리의 training 알고리즘의 근본적인 맹점을 노출한다는 것을 암시한다.
이러한 adversarial examples의 원인은 미스테리였으며, 추측에 의하면 DNN의 비선형성과, 불충분한 모델 정규화때문이라고 했다.
그러나, 고차원 공간에서 선형성은 adversarial examples을 유발했다. 즉, 비선형성이 adversarial examples의 원인이 아니다. 이러한 관점은 우리가 a fast method of generating adversarial examples을 설계할 수 있게 한다. 우리는 이것이 dropout만을 사용했을 때보다 더 추가적인 정규화를 제공할 수 있음을 보여준다.
3. THE LINEAR EXPLANATION OF ADVERSARIAL EXAMPLES
x˜ = x + η 에서 η(perturbation)가 매우 작을 경우, 분류기는 x와 x˜을 같은 class로 구분한다.
weight vector w와 an adversarial example x˜ 사이의 dot product는 다음과 같다.
adversarial perturbation은 wη 만큼 활성화의 증가를 야기한다. 우리는 max norm constraint에 따라 η=sign(w)으로 이 증가를 최대화 시킬 수 있다.
* max norm constraint
왜 max norm costraint인지에 대해서는 chapter 5에서 다룬다.
즉, η=εsign(w) 이라 할 때, wη = ε*w*sign(w) = ε||w|| 이고, w가 n 차원에, element의 절댓값 평균이 m이라 하면 이 값은 εmn이 된다.
예를 들어 w = [1,-2,3] 이라 하자.
그럼 sign(w) = [1,-1,1] 이고 이 둘의 내적은 1+2+3 = 6 이다.
즉 n이 3이고, w의 절대값 평균이 2이므로 3*2 = 6 이다.
따라서 wη은 차원 n에 비례하게 증가 할 수 있으며, 높은 차원의 문제에서 input에 작은 차이가 output에 큰 차이를 만들 수 있다. 즉, 높은 차원에서 input에 아주 작은 노이즈를 추가하여 Decision Boundary를 크게 넘길 수 있다.
이 설명은 input에 충분한 차원이 있는 경우, 간단한 선형 모델에 adversarial examples가 있을 수 있음을 보여준다.
4. LINEAR PERTURBATION OF NON-LINEAR MODELS
adversarial examples의 선형적인 견해는 그들을 생성하는 빠른 방법을 제안한다. 우리는 신경망이 adversarial perturbation에 저항하기에는 매우 선형적이라고 가정한다. LSTMs, ReLUs, maxout networks는 모두 최적화하기 쉽도록 매우 선형적인 방법으로 작동하도록 설계됐다. 즉, 이런 선형 동작이 신경망을 adversarial examples에 취약하도록 한다.
* ReLU
* 즉, NN은 생각보다 non-linear하지 않으며, linearity 때문에 adversarial 문제가 발생한다.
adversarial examples를 만드는 방법은 다음과 같다.
θ를 모델의 파라미터, x를 모델의 input, y를 target, J(θ, x, y)를 신경망 모델의 train cost function이라 할 때, noise는 다음과 같이 정의한다.
즉, NN에 기존의 x 대신 x + η(linearity) 를 추가하여 adversarial example을 만든다. 우리는 이것을 "fast gradient sign method" 라 한다. gradient는 backpropagation 으로 계산될 수 있다.
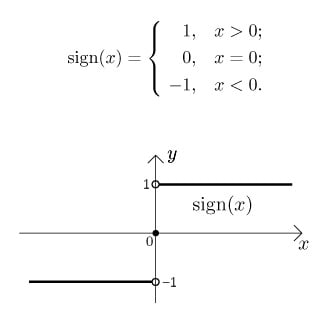
* sign(x) : 부호함수
원래는 cost의 기울기와 반대방향으로 움직여 cost를 0으로 만들도록 한다.
하지만, 기존의 input x 대신 x + η(cost gradient의 부호) 으로 오히려 cost를 크게하는 방향으로 update한다.
즉, 모델이 input을 제대로 분류하지 못하게 된다.
좀 더 쉽게 생각해서, 예를들어 1차원 공간에 빨간점과 파란점을 구분하는 상황이라 가정하자.
이 때, 빨간점을 기준으로 cost는 다음과 같다.
이 때의 cost의 기울기는 양수이며, 빨간점을 양수방향 즉, 오른쪽 방향으로 이동하면 빨간점은 Decision Boundary를 넘고, cost는 더 증가하게 된다.
파란점도 마찬가지로 cost의 기울기 방향 즉, 음수방향인 왼쪽으로 이동하면 Decision Boundary를 넘을 수 있다.
이 방법은 다양한 모델들에서 그들의 input을 잘 못 분류하도록 한다.
Figure 1은 InageNet 에 대한 GooleNet모델에 fast adversarial example generation을 적용했다. 아주 작은 noise를 첨가함으로써, GoogleNet이 해당 image를 잘못 분류하도록 했다. 이 때 ε은 0.007로 매우 작은 값이다.
ε = 0.25일 때, MINIST 데이터에 대해 평균 79.3%의 신뢰도로 99.9%의 error rate를 가졌다.
같은 환경에서, maxout 네트워크는 평균 97.6%의 신뢰도로 89.4% 잘 못 분류했다.
마찬가지로, ε = 0.1일 때, CIFAT-10 데이터에 대해 평균 96.6%의 신뢰도로 87.15% 오분류률을 가졌다.
이 단순하고 쉬운 알고리즘이 잘못 분류된 예제를 생성 할 수 있다는 사실은, adversarial examples가 선형성의 결과라는 증거이다. 알고리즘 또한 adversarial training의 속도를 높이거나, 훈련된 네트워크를 분석하는데 유용하다.
5. ADVERSARIAL TRAINING OF LINEAR MODELS VERSUS WEIGHT DECAY
아마도 우리가 고려할 수 있는 가장 간단한 분류 모델은 logistic regression 모델일 것이다. 이 경우, FGSM은 정확하다. 우리는 이 사례를 통해 이 간단한 방법이 어떻게 adversarial examples를 생성하는지 직관을 얻을 수 있다. Figure 2를 보자.
Figure 2 : FGSM을 logistic regression에 적용했다. a) 는 MINIST로 logistic regression model에 학습된 weight이다.
b) 는 MNIST로 학습된 모델 weight의 부호(+1,0,-1)이다. 이것이 최적의 pertubation(noise) 이다. c) MNIST 3과 7. 이 logistic model은 3과 7 분류에서 오직 1.6% 에러율을 가진다. d) logistic model에 ε = 0.25 일 때, Fast gradient sign adversarial examples. 이 예제들에 대해 99%의 에러율을 가진다.
label y ∈ {−1, 1} with P(y = 1) = σ(wx + b), σ(z) 은 logistic sigmoid function 일 때, cost function은
where ζ(z) = log (1 + exp(z)) is the softplus function.
* softplus function
softplus function이 무엇인지 이해하는 데에는 한참이 걸렸다. 사실 지금도 명백히 이해하진 못했다.
이해한 바에 의하면
1. classification 문제에서 cost function을 cross entropy가 아닌 softplus 라는 function을 쓴 이유는 y가 0,1이 아니라 -1,+1 이기 때문인 것 같다. 왜 y를 0,1이 아닌 -1,+1로 했는지는 아직도 이해하지 못했다.
2. softplus function이 무엇인지는 [Adversarial Training Versus Weight Decay] 논문에 나와있다.
논문 링크 : https://arxiv.org/pdf/1804.03308.pdf
(a) 는 wx+b에 대한 그림이다. 일반적으로 y가 0,1일 때는 wx+b를 0.5 기준으로 0 또는 1로 구분하지만, 이 경우에는 0을 기준으로 -1과 1로 구분한다.
(b) 는 wx+b에 y를 곱한 그림이다. 즉, 잘 구분한 것들은 양수로, 잘못 구분한 것들은 음수가 된다.
(c) 따라서 잘못 구분된 것들의 cost는 매우 높고, 잘 구분된 것들의 cost는 0이 된다.
위 식에 x 대신 gradient sign perturbation에 근거한 x의 adversarial perturbation을 적용하면 다음과 같은 식이 된다.
즉, x 대신 cost의 gradient방향만큼 더한 x + η를 대입하면 다음과 같다.
이 때,
인 이유는 (이 부분은 확실하지 않다.)
이는 L1 regularization과 비슷해보인다.(||w||1 때문인 듯 하다.) 그러나, 몇 가지 중요한 차이점이 있다. L1은 일반적으로 feature selection의 기능이 있다. 즉, input이 다차원일 때, 모든 차원에 대해서 조금씩 움직이는 것이 아니라, 몇 개의 차원에 대해 크게 움직인다.
예를들어, 2차원의 공간에서 input x를 x+η 로 update한다고 가정하자. 이 때, x+η는 x와 눈으로 보기에는 같은 class여야 하며, Decision Boundary는 넘어야 한다.
왼쪽에 Max norm의 경우 모든 차원에 대해 조금씩 움직여 Desicion Boundary는 넘었지만, 원래의 input과 큰 차이 없어 보인다. 그에 반해 오른쪽 L1 norm의 경우 x1에 대해서만 크게 움직였다.
2차원 공간에서는 왼쪽과 오른쪽이 큰 차이 없어 보일 수도 있지만, 더 큰 차원이라고 생각하면 이해가 될 것이다.
6. ADVERSARIAL TRAINING OF DEEP NETWORKS
deep network는 얕은 선형모델과 달리, adversarial perturbation에 저항할 기능이 있다.
Szegedy는 adverarial과 깨끗한 데이터를 섞어서 학습함으로서, 신경망 모델이 다소 정규화 될 수 있음을 보였다. adversarial examples는 일반적인 data augmentation과는 다르다. (일반적인 data augmentation은 test set에 실제로 발생할 것 같은 방식으로 변환한다.) 이런 adversarial examples과 같은 형태의 data augmentation은 자연스러운 input은 아니지만, model의 결함을 보완할 수 있다.
우리는 FGSM에 근거한 정규화에 효율적인 adversarial objective function을 찾았다.
FGSM으로 만들어진 adversarial example에 대해 adversarial training 없이는 89.4%의 error rate였으나, adversarial training로 error rate는 17.9%로 떨어졌다.
Figure 3 : adversarial training으로 훨씬 정규화 되었음을 볼 수 있다.
느낀점 : 이런건 왜 만드는건가.. 범죄용..?



















