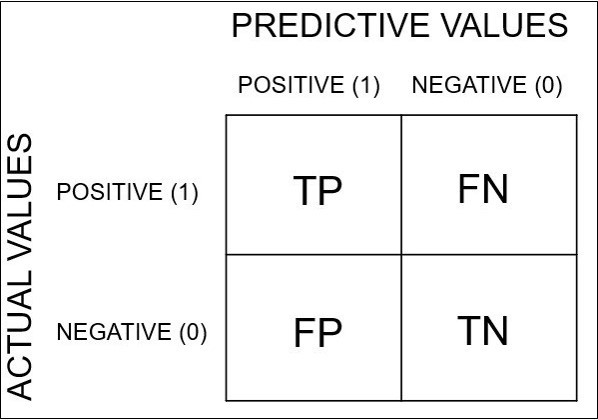
분류 모델 성능 평가 지표 Linear 모델에 대해서는 R-Square, MSE 등 으로 모델의 성능을 평가한다.그렇다면 분류 모델에 대해서는 모델의 성능을 어떻게 평가할 수 있을까? 여러가지 방법이 있지만, 대표적으로 사용하는 정확도(Accuracy), 정밀도(Precision), 재현도(Recall), F1 Score 에 대해 알아보고자 한다. 1. Confusion Matrix (오차행렬) 위 네가지 지표를 설명하기 전에 Confusion Matrix를 먼저 설명하고자 한다. Confusion Matrix란? Training 을 통한 Prediction 성능을 측정하기 위해 예측 value와 실제 value를 비교하기 위한 표 여기서 ACTUAL VALUES는 실제값, PREDICTIVE VALUE..