슈퍼짱짱

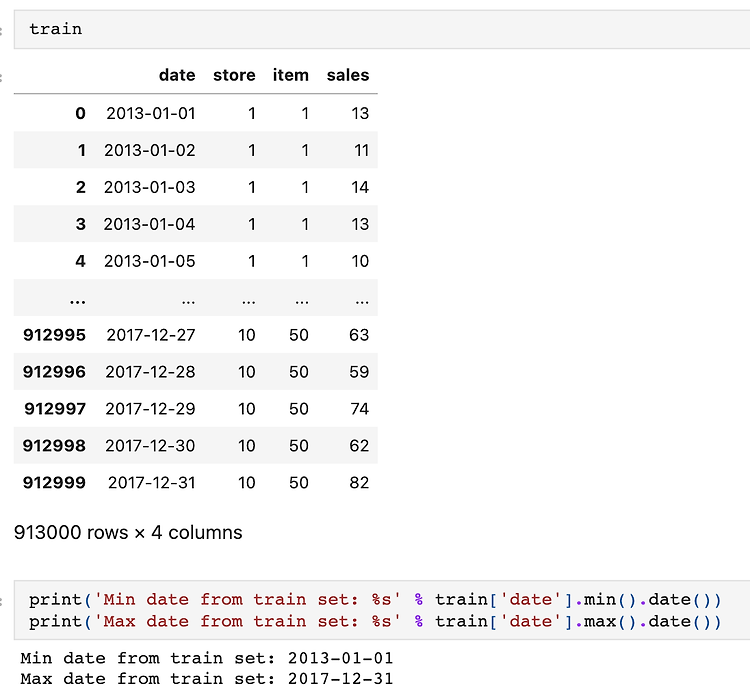
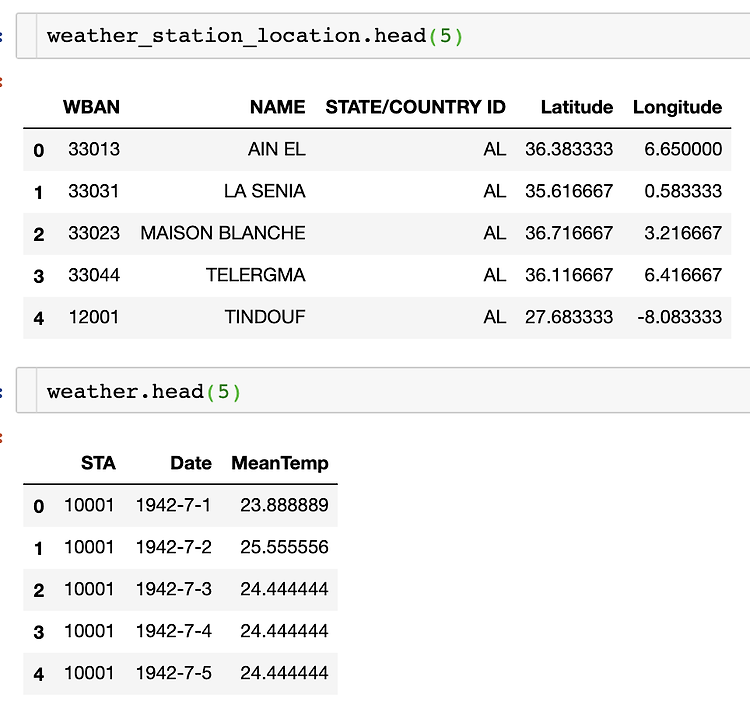
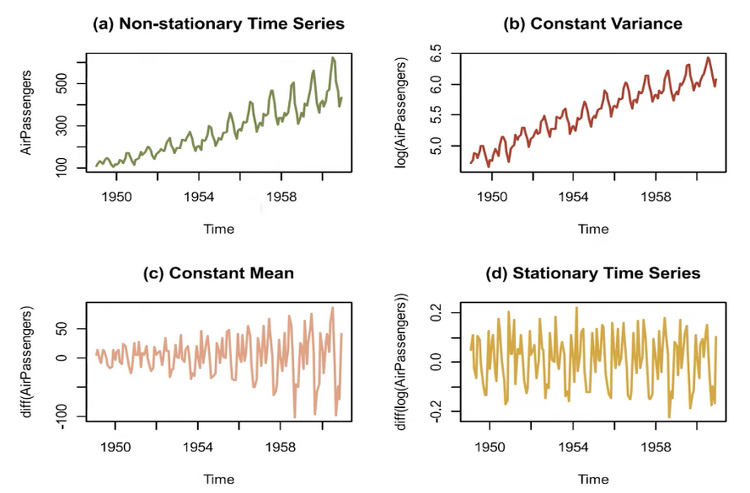
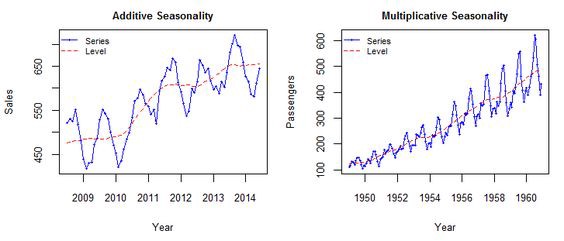
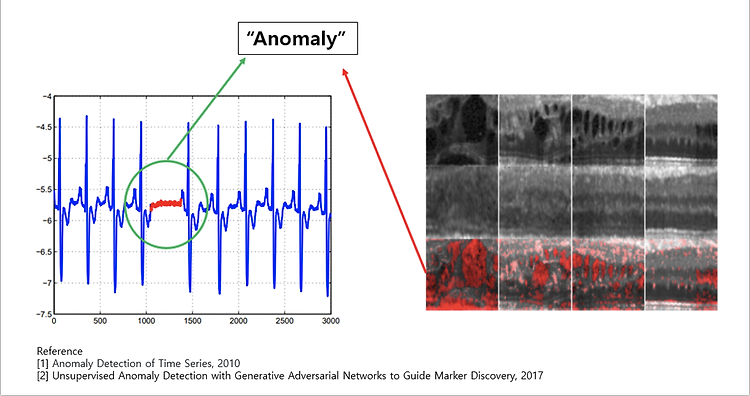
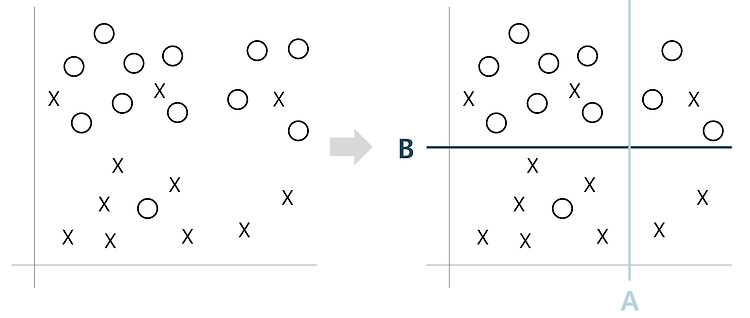
2020년 4월에 ICLR 개재된 RaPP를 Tensorflow로 구현해보았다. 논문 링크 : https://openreview.net/forum?id=HkgeGeBYDB RaPP: Novelty Detection with Reconstruction along Projection Pathway A new methodology for novelty detection by utilizing hidden space activation values obtained from a deep autoencoder. openreview.net 참고 링크 : https://makinarocks.github.io/rapp/ RaPP - Novelty Detection with Reconstruction along Proje..

2021.05.24 - [통계 지식/시계열자료 분석] - 시계열 분해란?(Time Series Decomposition) :: 시계열 분석이란? 시계열 데이터란? 추세(Trend), 순환(Cycle), 계절성(Seasonal), 불규칙 요소(Random, Residual) 시계열 분해란?(Time Series Decomposition) :: 시계열 분석이란? 시계열 데이터란? 추세(Trend), 순환(Cycle), 시계열 데이터란? 시간에 순차적으로 관측한 값들의 집합이며, 예측 모델에서 시간을 변수로 사용하는 특징이 있다. 시계열 데이터 분석이란? 과거 데이터의 패턴을 분석하여 미래의 값을 예측 leedakyeong.tistory.com 2021.05.24 - [통계 지식/시계열자료 분석] - ARIM..

2021.05.24 - [통계 지식/시계열자료 분석] - 시계열 분해란?(Time Series Decomposition) :: 시계열 분석이란? 시계열 데이터란? 추세(Trend), 순환(Cycle), 계절성(Seasonal), 불규칙 요소(Random, Residual) 시계열 분해란?(Time Series Decomposition) :: 시계열 분석이란? 시계열 데이터란? 추세(Trend), 순환(Cycle), 시계열 데이터란? 시간에 순차적으로 관측한 값들의 집합이며, 예측 모델에서 시간을 변수로 사용하는 특징이 있다. 시계열 데이터 분석이란? 과거 데이터의 패턴을 분석하여 미래의 값을 예측 leedakyeong.tistory.com 2021.05.24 - [통계 지식/시계열자료 분석] - ARIM..

앞 서, 시계열 데이터와 시계열 분석에 대한 간단한 설명과 시계열 분해법에 대해 설명했다. 2021.05.24 - [통계 지식/시계열자료 분석] - 시계열 분해란?(Time Series Decomposition) :: 시계열 분석이란? 시계열 데이터란? 추세(Trend), 순환(Cycle), 계절성(Seasonal), 불규칙 요소(Random, Residual) 시계열 분해란?(Time Series Decomposition) :: 시계열 분석이란? 시계열 데이터란? 추세(Trend), 순환(Cycle), 시계열 데이터란? 시간에 순차적으로 관측한 값들의 집합이며, 예측 모델에서 시간을 변수로 사용하는 특징이 있다. 시계열 데이터 분석이란? 과거 데이터의 패턴을 분석하여 미래의 값을 예측 leedakyeo..

시계열 데이터란? 시간에 순차적으로 관측한 값들의 집합이며, 예측 모델에서 시간을 변수로 사용하는 특징이 있다. 시계열 데이터 분석이란? 과거 데이터의 패턴을 분석하여 미래의 값을 예측하는 방법으로, 과거의 패턴이 미래에도 지속된다는 데이터의 안정성이 기본적인 가정으로 필요하다. 시계열 분해법이란? What is Time Series Decomposition? 시계열 데이터를 추세/순환/계절/불규칙 요소로 분해하는 기법이다. 추세(Trend)란? 데이터가 장기적으로 증가하거나 감소하는 것이며, 추세가 꼭 선형적일 필요는 없다. 순환(Cycle)이란? 경기변동과 같이 정치, 경제, 사회적 요인에 의한 변화로, 일정 주기가 없으며 장기적인 변화 현상이다. 계절성(Seasoanl)이란? 주, 월, 분기, 반기..

Auto Encoder로 Anomaly Detection 하는 방법 설명 및 Kaggle 사례 소개 오토인코더로 이상치를 탐지하는 방법에 대해 설명하기에 앞서, 이상 탐지가 무엇인지 간단히 설명하겠다. 1. Anomaly Detection이란? Normal(정상) Sample과 Abnomal(비정상, 이상치, 특이치) Sample을 구별해내는 문제로, 제조업/CCTV/의료 영상/Social Network 등 다양한 분야에서 응용되고 있다. 출처 : github.com/hoya012/awesome-anomaly-detection 위 그림에서 왼쪽 그림은 시계열 데이터로, 일정 주기로 일정 패턴을 보이다가 이상치를 보이는 부분이 있다. 오른쪽 그림은 이미지 데이터로, 역시 이상치를 보이는 부분이 있으며, 이..

R에서 GA 최대값으로 최적화 하지 않고, 지정된 값으로 최적화 하는 방법 Genetic Algorithm(GA - 유전 알고리즘) 최적화 문제를 해결하는 기법 중 하나로, 생물의 진화를 모방한 방법이다. R에서는 GA 패키지로 제공되고 있으며, 기본적으로 주어진 fitness function을 최대화 하는 방향으로 최적화 한다. (function에 -(minus)를 붙여주면 최솟값으로 최적화 할 수도 있다. 자세한 방법은 아래 실습에서 다루겠다.) 1. Maximizing 우선, 주어진 function을 최대화 하는 기본적인 코드는 다음과 같다. 주어진 function은 다음과 같고, 찾고자 하는 x의 범위는 -10 ~ 10라 하자. $$function : (x^2+x)*cos(x)$$ 해당 fun..

2020/04/21 - [통계 지식/Algorithm] - Decision Tree란? :: ID3 알고리즘, 엔트로피란? Decision Tree란? :: ID3 알고리즘, 엔트로피란? 의사결정나무란? Decision Tree란? 의사결정 규칙을 나무구조로 나타내에 전체 데이터를 소집단으로 분류하거나 예측하는 분석기법 전체 데이터에서 마치 스무고개하듯이 질문하며 분류해나간다. 그 모양이 마치.. leedakyeong.tistory.com 2020/04/21 - [통계 지식/Algorithm] - 의사결정나무(Decision Tree) :: CART 알고리즘, 지니계수(Gini Index)란? 의사결정나무(Decision Tree) :: CART 알고리즘, 지니계수(Gini Index)란? 이전 포스팅에..

2020/04/21 - [통계 지식/Algorithm] - Decision Tree란? :: ID3 알고리즘, 엔트로피란? Decision Tree란? :: ID3 알고리즘, 엔트로피란? 의사결정나무란? Decision Tree란? 의사결정 규칙을 나무구조로 나타내에 전체 데이터를 소집단으로 분류하거나 예측하는 분석기법 전체 데이터에서 마치 스무고개하듯이 질문하며 분류해나간다. 그 모양이 마치.. leedakyeong.tistory.com 2020/04/21 - [통계 지식/Algorithm] - 의사결정나무(Decision Tree) :: CART 알고리즘, 지니계수(Gini Index)란? 의사결정나무(Decision Tree) :: CART 알고리즘, 지니계수(Gini Index)란? 이전 포스팅에..

이전 포스팅에서 의사결정나무란 무엇인지, 어떤 기준으로 모델을 만들어가며 불순도가 무엇인지와 ID3 알고리즘에 대해 소개했다. 지난 포스팅 바로가기 https://leedakyeong.tistory.com/entry/Decision-Tree%EB%9E%80-ID3-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98 Decision Tree란? :: ID3 알고리즘, 엔트로피란? 의사결정나무란? Decision Tree란? 의사결정 규칙을 나무구조로 나타내에 전체 데이터를 소집단으로 분류하거나 예측하는 분석기법 전체 데이터에서 마치 스무고개하듯이 질문하며 분류해나간다. 그 모양이 마치.. leedakyeong.tistory.com 이번에는 의사결정나무의 또 다른 알고리즘인 CART 알고리즘에..