슈퍼짱짱

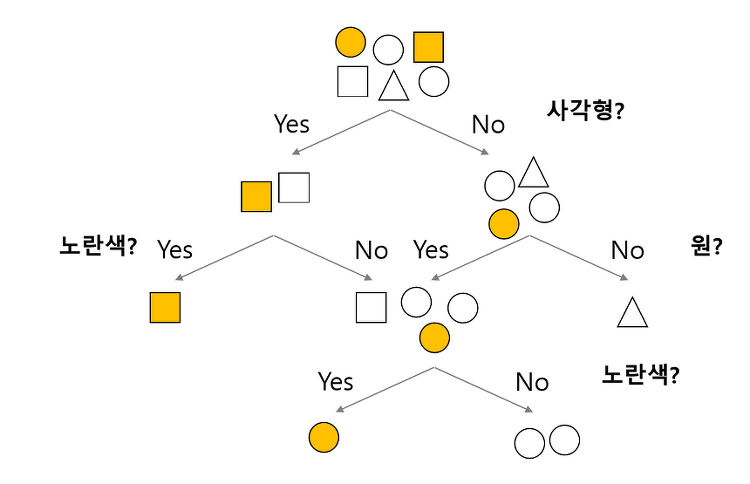
의사결정나무란? Decision Tree란? 의사결정 규칙을 나무구조로 나타내에 전체 데이터를 소집단으로 분류하거나 예측하는 분석기법 전체 데이터에서 마치 스무고개하듯이 질문하며 분류해나간다. 그 모양이 마치 나무와 같아서 의사결정 나무라 부른다. 예) 나무에서 분할되는 부분을 노드(node) 라 하고, 가장 처음 노드를 root node, 가장 마지막 노드들을 terminal node라 한다. 그렇다면, 위의 예시에서 모양 or 색 중에서 무엇을 먼저, 어떤 기준으로 나눠야 할까? 그 답은 불순도가 낮아지는 방향으로 나눠야 하며, 그 방법으로 ID3, CART, C4.5 등 여러 알고리즘이 있다. 본 포스팅에서는 ID3에 대해 알아보고자 한다. ID3 알고리즘에 대해 알아보기에 앞서, 불순도란 무엇이며..

분류 모델 성능 평가 지표 Linear 모델에 대해서는 R-Square, MSE 등 으로 모델의 성능을 평가한다.그렇다면 분류 모델에 대해서는 모델의 성능을 어떻게 평가할 수 있을까? 여러가지 방법이 있지만, 대표적으로 사용하는 정확도(Accuracy), 정밀도(Precision), 재현도(Recall), F1 Score 에 대해 알아보고자 한다. 1. Confusion Matrix (오차행렬) 위 네가지 지표를 설명하기 전에 Confusion Matrix를 먼저 설명하고자 한다. Confusion Matrix란? Training 을 통한 Prediction 성능을 측정하기 위해 예측 value와 실제 value를 비교하기 위한 표 여기서 ACTUAL VALUES는 실제값, PREDICTIVE VALUE..

로지스틱 회귀분석이란? 지난 시간 언젠가 수치형자료와 범주형자료에 대해 다룬 적이 있다. >> 수치형 자료, 범주형 자료 바로가기 2019/08/12 - [통계 지식/기초통계] - [기초통계] 수치형 자료(numerical data)와 범주형 자료(categorical data) 2019/08/12 - [통계 지식/기초통계] - [기초통계] 수치형 자료(numerical data)와 범주형 자료(categorical data) 종속변수가 수치형 자료형일 때 Linear Regression으로 모델링한다면, 범주형 자료 중에서도 Binary(0 or 1로 표현할 수 있는 범주형 변수 ex- 남/여, 성공/실패, 합격/불합격 등) 일 때 Logistic Regression으로 Y에 대한 예측 모델을 만들 수..

넬슨법칙이란? Nelson Rules 는 공정에서 발생할 수 있는 불량(측정 변수가 제어 범위를 벗어났는지 or non-random)의 조건을 파악하기 위한 방법이다. 일반적으로 좋은 공정이란 측정된 값이 일정 범위 이내에 있으며, random 한 형태로 존재하는 것이다. Nelson Rule에서는 그렇지 못한 경우를 불량이라 정의하고, 그러한 패턴을 찾기 위해 만들어졌다. 불량을 판단하는 기준에는 총 8가지 Rule이 있으며, 각각에 대한 설명은 다음과 같다.* 단, UCL/LCL의 default값은 측정 값들의 평균 +-3 시그마이며, 이는 parameter로 조정될 수 있다. 1. Rule 1 : 측정된 값이 평균 + 3 시그마를 벗어난 경우. 2. Rule 2 : 연속적으로 관측된 9개 이상의 점..

이전에 두 모집단이 독립 일 때 모평균을 비교하는 방법에 대해 알아보았다.이번에는 두 모집단이 독립이 아닐 때 모평균을 비교하는 방법인 짝비교에 대해 알아보겠다. >> 모평균 비교 바로가기>> 두 모집단이 독립일 때 :: 표본의 크기가 클 때 >> 두 모집단이 독립일 때 :: 표본의 크기가 작을 때(1)>> 두 모집단이 독립일 때 :: 표본의 크기가 작을 때(2) 독립이 아닌 두 모집단에서 모평균 비교하는 방법 :: 짝비교 두 종류의 처리효과를 비교할 때, 반응값들의 차이가 처리효과의 차이에 의해서만 발생하도록 실험단위들이 비슷한 조건을 갖는 것이 이상적이다. 그러나, 실제로는 이 조건을 만족시키기가 어렵다. 예를 들어, 두 진통제의 효과를 비교하기 위해 성별, 나이, 건강상태 등이 모두 동일한 환자들을..

독립인 두 모집단에서 표본의 크기가 작을 때 모평균의 차 ($\mu_{1} - \mu_{2}$) 비교 표본의 크기가 작을 때는 일반적으로 두 모집단에 대하여 정규분포 가정이 필요하다. 또 다른 가정은 ① 두 모집단의 표준편차가 같다고 가정하는 경우와 ② 두 모집단의 표준편차가 다르다고 가정하는 경우이다. 이전 포스팅에서 독립인 두 모집단에서 표본의 크기가 작을 때, 모표준편차가 같은 경우에 대한 모평균 비교 방법에 대해 알아보았다. 이번에는 모표준편차가 다를 때 모평균 비교 검정 방법에 대해 알아보겠다. >> 독립인 두 모집단에서 표본의 크기가 작을 때 바로가기 2. 두 모집단의 표준편차가 다른 경우 * 독립인 두 모집단에서 표본의 크기가 작고 두 모표준편차가 다를 때, 모평균의 차 (\(\mu_{1..

이전에 독립인 두 모집단에서 표본의 크기가 클 때 모평균 비교 검정하는 방법에 대해 알아보았다. 이번에는 표본의 크기가 작을 때 모평균 비교 검정하는 방법을 알아보겠다. >> 독립인 두 모집단에서 표본의 크기가 클 때 바로가기 독립인 두 모집단에서 표본의 크기가 작을 때 모평균의 차 ($\mu_{1} - \mu_{2}$) 비교 표본의 크기가 작을 때는 일반적으로 두 모집단에 대하여 정규분포 가정이 필요하다. 또 다른 가정은 ① 두 모집단의 표준편차가 같다고 가정하는 경우와 ② 두 모집단의 표준편차가 다르다고 가정하는 경우이다. 1. 두 모집단의 표준편차가 같다고 가정하는 경우 두 모집단의 표준편차가 같은지($\sigma_{1} = \sigma_{2}$) 판단하기 위해 표본표준편차를 이용한다. 두 ..

이전 포스팅에서 자료수집과정에 따른 두 모집단 비교 방법에 대해 알아보았다.이번에는 그 중 두 모집단이 독립일 경우에 모평균 차이를 추론하는 방법에 대해 알아보겠다. >> 두 모집단 비교 방법 바로가기 두 개의 독립 표본에서 모평균 차이 추론하는 방법 우선 두 모집단으로부터 추출된 표본과 그로부터 계산되는 통계량은 다음과 같다. $X_{1}, \cdots, X_{n_{1}}$ : 평균이 $\mu_{1}$이고 표준편차가 $\sigma_{1}$인 모집단으로부터 추출된 표본$\bar{X} = \frac{1}{n_{1}} \sum_{i=1}^{n_{1}} X_{i}$, $s^2_{1} = \frac{1}{n_{1}-1} \sum_{i=1}^{n_{1}} (X_{i}-\bar{X})^2$ \(Y..

이전에는 하나의 모집단에 대한 모평균을 추론하는 방법에 대해 알아보았다. 이번에는 하나의 모집단에 관한 것 뿐 아니라 두 모집단 간의 차이를 검정하는 방법에 대해 알아보겠다. 예) 두 종류의 강의방법에 의한 학습효과 비교기촌의 치료약과 새롭게 개발된 치료약의 효능 비교 두 모집단의 비교 두 모집단의 비교를 위한 추론과정은 자료를 어떻게 수집하느냐에 따라 추론방법이 달라지게 되는데, 대표적인 두 종류의 자료수집과정에 따른 추론방법을 알아보겠다. 1. 실험단위가 독립인 경우 예) 새로 개발된 치료약의 효능이 기존의 약보다 좋음을 검증하기 위해 건강상태가 비슷한 19마리의 쥐를 대상으로 병균을 투입한 후, 그 중에서 임의로 10마리의 쥐를 추출하여 그들에게는 기존의 약을 투약하고, 나머지 쥐들에게는 새로운 약..

t-분포 이전에 표본의 크기가 큰 경우(30 이상)에 적용할 수 있는 모평균 $\mu$에 대한 추론방법을 알아보았다. 표본의 크기가 큰 경우에는 중심극한정리에 의해 표본평균 $\bar{X}$의 분포가 정규분포가 된다는 사실을 이용했다. 그러나, 표본의 크기가 작을 때에는 표본평균 $\bar{X}$의 분포는 모집단의 분포에 많은 영향을 받는다. 모집단의 분포가 $N(\mu, \sigma^2)$일 때 크기가 $n$인 표본의 평균 $\bar{X}$의 분포는 정확하게 $N(\mu, \sigma^2/n)$이다. 따라서 이를 표준화시키면 $$\frac{\bar{X}-\mu}{\sigma/\sqrt n} ~ N(0, 1)$$ 이 된다. 그러나 일반적으로 $\sigma$는 미지수이기 때문에..