시계열 분해란?(Time Series Decomposition) :: 시계열 분석이란? 시계열 데이터란? 추세(Trend), 순환(Cycle),
시계열 데이터란? 시간에 순차적으로 관측한 값들의 집합이며, 예측 모델에서 시간을 변수로 사용하는 특징이 있다. 시계열 데이터 분석이란? 과거 데이터의 패턴을 분석하여 미래의 값을 예측
leedakyeong.tistory.com
2021.05.24 - [통계 지식/시계열자료 분석] - ARIMA란? :: ARIMA 분석기법, AR, MA, ACF, PACF, 정상성이란?
ARIMA란? :: ARIMA 분석기법, AR, MA, ACF, PACF, 정상성이란?
앞 서, 시계열 데이터와 시계열 분석에 대한 간단한 설명과 시계열 분해법에 대해 설명했다. 2021.05.24 - [통계 지식/시계열자료 분석] - 시계열 분해란?(Time Series Decomposition) :: 시계열 분석이란? 시
leedakyeong.tistory.com
2021.05.25 - [통계 지식/시계열자료 분석] - [Python] 날씨 시계열 데이터(Kaggle)로 ARIMA 적용하기
[Python] 날씨 시계열 데이터(Kaggle)로 ARIMA 적용하기
2021.05.24 - [통계 지식/시계열자료 분석] - 시계열 분해란?(Time Series Decomposition) :: 시계열 분석이란? 시계열 데이터란? 추세(Trend), 순환(Cycle), 계절성(Seasonal), 불규칙 요소(Random, Residual) 시..
leedakyeong.tistory.com
이전에 시계열 데이터 분석 기법 중 ARIMA에 대해 자세히 알아보았고, 실제 데이터로 파이썬 코드도 짜보았다.
이번에는 MLP, CNN, LSTM 등 Deep Learning 알고리즘으로 시계열 분석하는 코드를 포스팅하겠다.
딥러닝(MLP, CNN, LSTM, CNN+LSTM)으로 시계열 분석하기
분석할 시계열 데이터는 Sales 데이터로, kaggle에 Store Item Demand Forecasting Challenge Competition에 제공된 데이터이며, Train Set과 Test Set으로 나뉘어져있는 csv 파일이다.
Train Set은 총 913000개의 행, 4개의 열이고,
Test Set은 총 45000개의 행, 4개의 열로 이루어져 있다.
Train Set은 date, store, item, sales로 이루어져 있으며, 각 컬럼은 다음과 같다.
date : 날짜(Date of the sale data. There are no holiday effects or store closures.)
store : Store ID(1~10)
item : Item ID(1~50)
sales : 판매량(Number of items sold at a particular store on a particular date.)
Test Set은 sales 컬럼이 없고, id 컬럼이 있다.(id는 정답 체점 시 key가 되는 값이다.)
(Test Set에 대한 정답지가 공개되어있지 않으므로, 이후 Modeling에서는 Train Set에서 Validation Set을 나누어 Validation Set으로 성능을 확인한다.)
kaggle에 올라와있는 코드를 참고했다.
1. Import Library
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow
from tensorflow.keras import optimizers
from tensorflow.keras.utils import plot_model
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.layers import Conv1D, MaxPooling1D
from tensorflow.keras.layers import Dense, LSTM, RepeatVector, TimeDistributed, Flatten
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
import plotly.graph_objs as go
from plotly.offline import init_notebook_mode, iplot
%matplotlib inline
warnings.filterwarnings("ignore")
init_notebook_mode(connected=True)
# Set seeds to make the experiment more reproducible.
from tensorflow import set_random_seed
from numpy.random import seed
set_random_seed(1)
seed(1)2. Data
train = pd.read_csv('../01. Data/train.csv', parse_dates=['date'])
test = pd.read_csv('../01. Data/test.csv', parse_dates=['date'])
Train Set은 store 10개, item 50개에 따른 날짜 별 Sales 데이터이며, 2013년 1월 1일부터 2017년 12월 31일까지 총 5년에 해당하는 Daily 데이터이다.

Test Set은 sales 컬럼 대신 id가 포함되어 있으며, 2018년 1월 1일부터 2018년 3월 31일까지 총 90일에 해당하는 데이터이다.

3. EDA
Train Set의 Sales 값을 일별 합, 일별 Store별 합, 일별 Item별 합으로 그래프를 그려보면 다음과 같다.
daily_sales = train.groupby('date', as_index=False)['sales'].sum()
store_daily_sales = train.groupby(['store', 'date'], as_index=False)['sales'].sum()
item_daily_sales = train.groupby(['item', 'date'], as_index=False)['sales'].sum()
3-1. 일별 총 판매량
plt.figure(figsize=(20,8))
plt.plot(daily_sales['date'],daily_sales['sales'])
plt.title('Daily sales')
plt.xlabel('Date')
plt.ylabel('Sales')
3-2. 일별, Store별 총 판매량
plt.figure(figsize=(20,8))
for i in range(1,11) :
temp = store_daily_sales[store_daily_sales.store==i]
plt.plot(temp['date'],temp['sales'], label = 'Store %d' % i)
plt.legend()
plt.title('Store Daily Sales')
plt.xlabel('Date')
plt.ylabel('Sales')
3-3. 일별, Item별 총 판매량
plt.figure(figsize=(20,8))
for i in range(1,51) :
temp = item_daily_sales[item_daily_sales.item==i]
plt.plot(temp['date'],temp['sales'], label = 'Item %d' %i)
# plt.legend()
plt.title('Item Daily Sales')
plt.xlabel('Date')
plt.ylabel('Sales')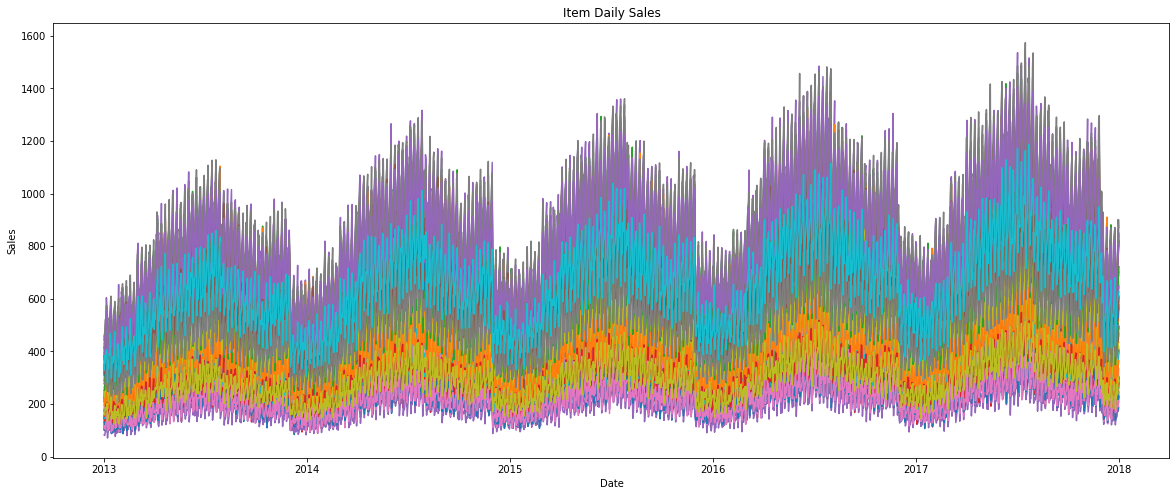
item은 50개나 되기때문에 그래프에 legend를 따로 표시하지 않았다.
전반적으로 미세하게 우상향하는 Trend가 보이며, 1년 단위로 계절성이 뚜렷하게 보인다.
참고로 각각의 그래프를 그리기 위한 daily_sales, store_daily_sales, item_daily_sales 는 다음과 같다.
daily_sales

store_daily_sales
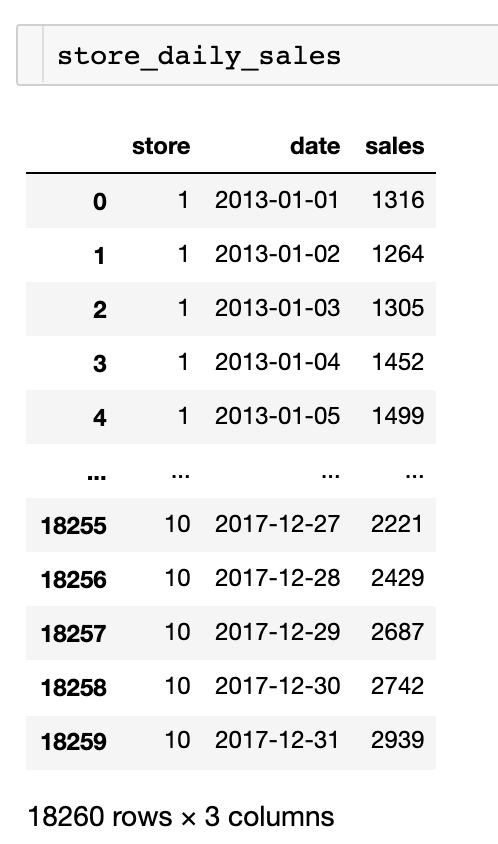
item_daily_sales
4. 전처리
4-1. Train only the last year
2013-01-01 ~ 2017-12-31 중 2017년 데이터만 활용해서 Train 한다.
train = train[(train['date'] >= '2017-01-01')]
4-2. Transform the data into a time series problem
Time Series 문제에 맞게 데이터 형태를 변환한다.
30일치로 90일 뒤를 학습한다.
예로, 2017-09-04 ~ 2017-10-03 판매량으로 2018-01-01 판매량을 학습하고,
2017-09-05 ~ 2017-10-04 판매량으로 2018-01-02 판매량을 학습한다.
X값과 Y값과의 차이가 90일이나 나는 이유는 Test Set이 90일치이기 때문이다.
2018-01-01 ~ 03-31까지의 데이터가 Test Set이므로 Y값이 없기 때문에
3월 30일 데이터로 3월 31일 값을 예측할 수 없으므로, 가지고 있는 데이터 중 가장 최근 데이터인 2017년 12월 31일 데이터로 2018년 3월 31일 값을 예측해야 한다. 이 둘의 차이가 바로 90일이다.
def series_to_supervised(data, window=1, lag=1, dropnan=True):
cols, names = list(), list()
# Input sequence (t-n, ... t-1)
for i in range(window, 0, -1):
cols.append(data.shift(i))
names += [('%s(t-%d)' % (col, i)) for col in data.columns]
# Current timestep (t=0)
cols.append(data)
names += [('%s(t)' % (col)) for col in data.columns]
# Target timestep (t=lag)
cols.append(data.shift(-lag))
names += [('%s(t+%d)' % (col, lag)) for col in data.columns]
# Put it all together
agg = pd.concat(cols, axis=1)
agg.columns = names
# Drop rows with NaN values
if dropnan:
agg.dropna(inplace=True)
return agg
train_gp = train.sort_values('date').groupby(['item', 'store', 'date'], as_index=False)
train_gp = train_gp.agg({'sales':['mean']})
train_gp.columns = ['item', 'store', 'date', 'sales']
window = 29
lag = lag_size
series = series_to_supervised(train_gp.drop('date', axis=1), window=window, lag=lag)
last_item = 'item(t-%d)' % window
last_store = 'store(t-%d)' % window
series = series[(series['store(t)'] == series[last_store])]
series = series[(series['item(t)'] == series[last_item])]
columns_to_drop = [('%s(t+%d)' % (col, lag)) for col in ['item', 'store']]
for i in range(window, 0, -1):
columns_to_drop += [('%s(t-%d)' % (col, i)) for col in ['item', 'store']]
series.drop(columns_to_drop, axis=1, inplace=True)
series.drop(['item(t)', 'store(t)'], axis=1, inplace=True)
하루씩 shift하여 총 29일치를 shift하고, 90일 이후 값을 붙여준다.
즉, t 시점을 기준으로 (t-29 ~ t)시점까지의 값이 X값이고, (t+90) 시점의 값이 Y값이다.

위 데이터를 날짜로 확인해보면 다음과 같다.
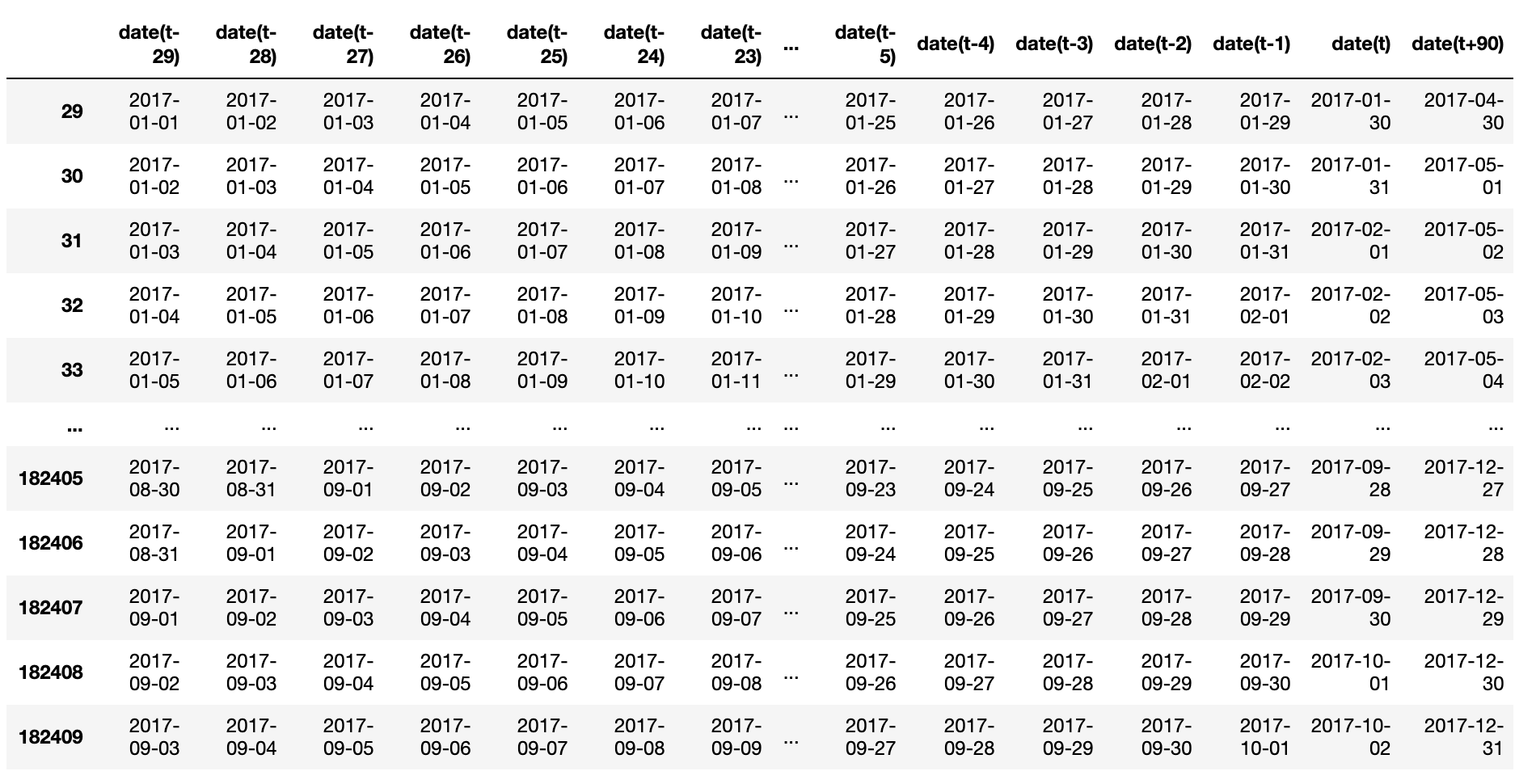
첫 번째 행 기준으로 2017-01-01 ~ 2017-01-30 시점의 한달치 판매량 데이터로 2017-04-30 시점의 판매량을 학습할 수 있도록 만들어졌다.
단, 위 데이터는 10개의 Store와 50개의 Item이 포함된 데이터이지만,
item=1, store=1에 대해 365일 판매량이 쭉 붙어있고,
그 아래 이어서 item=1, store=2에 대한 365일 판매량이 쭉 붙어 있는 형태이다.
따라서 하나씩 shift 했을 때 대부분의 데이터가 같은 item, 같은 store에 대한 값이므로, item과 store가 바뀌는 포인트를 따로 고려하여 처리하지 않은 듯 하다.
store가 1에서 2로 넘어갈 때 date는 12월 31일에서 다시 1월 1일이 된다.

5. Train/Validation Split
sklearn 패키지에 train_test_split 함수를 활용하여 random하게 나누었다.
train 60 : validation 40
# Label
labels_col = 'sales(t+%d)' % lag_size # sales(t+90)
labels = series[labels_col]
series = series.drop(labels_col, axis=1)
X_train, X_valid, Y_train, Y_valid = train_test_split(series, labels.values, test_size=0.4, random_state=0)
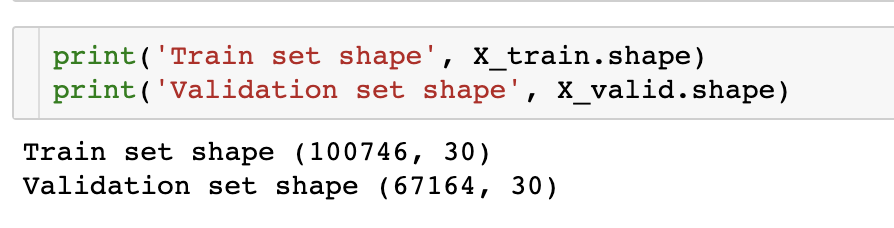
6. MLP
모델에 적용하기에 앞 서, 파라미터 몇 가지를 설정해 준다.
epochs = 40
batch = 256
lr = 0.0003
adam = optimizers.Adam(lr)
40번 반복학습하고, 한 번에 256개씩 학습하며, learning rate는 0.0003으로 설정했다.
optimizer는 adam을 사용한다.
Model Arichtecture는 다음과 같다.
model_mlp = Sequential()
model_mlp.add(Dense(100, activation='relu', input_dim=X_train.shape[1]))
model_mlp.add(Dense(1))
model_mlp.compile(loss='mse', optimizer=adam)

이를 그림으로 도식화 하면 다음과 같다.

30일치 데이터 \(x_0 \)~ \(x_{29}\) 가 input으로 들어가고, 100의 뉴런을 가진 hidden layer하나, 그리고 1개의 output이다.
input layer에서 hidden layer가 계산되는 부분을 확대해보면 다음과 같다.
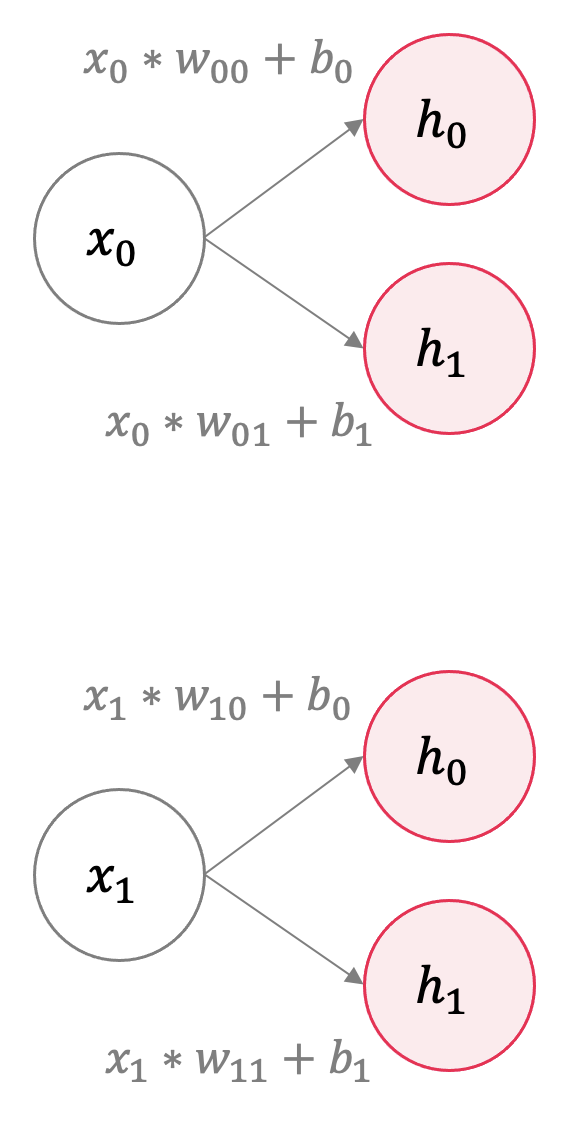
\(x_0\)가 \(h_0\)로 계산되기 위해 하나의 weight를 곱해주고 하나의 bias를 더해준다.
즉, 필요한 Parameter 수는 (1X30)의 input layer에서 (1X100)의 hidden layer로 계산되기 위해 (30X100)의 Weight와 (1X100)의 Bias가 필요하다. 즉, Dense(100)까지 3100개의 파라미터가 필요하다.
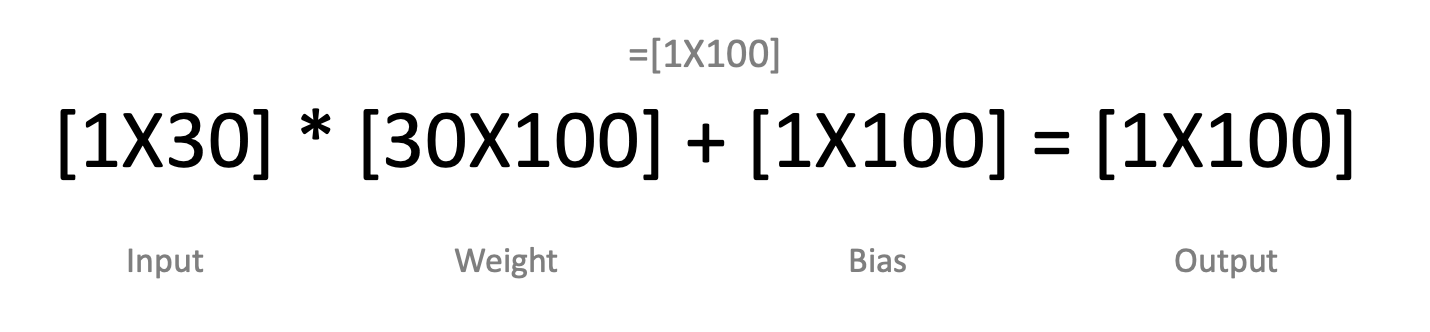
학습하고, Prediction한 결과는 다음과 같다.
mlp_history = model_mlp.fit(X_train.values, Y_train, validation_data=(X_valid.values, Y_valid), epochs=epochs, verbose=2)
mlp_train_pred = model_mlp.predict(X_train.values)
mlp_valid_pred = model_mlp.predict(X_valid.values)
Y_train_ = pd.DataFrame({'y_true': Y_train, 'y_pred': mlp_train_pred.reshape(mlp_train_pred.shape[0],)}).set_index(X_train.index).sort_index()
Y_train_ = pd.merge(Y_train_, train_gp,
left_index=True, right_index=True,
how='left')
Y_valid_ = pd.DataFrame({'y_true': Y_valid, 'y_pred': mlp_valid_pred.reshape(mlp_valid_pred.shape[0],)}).set_index(X_valid.index).sort_index()
Y_valid_ = pd.merge(Y_valid_, train_gp,
left_index=True, right_index=True,
how='left')

scorring 함수는 다음과 같다.
from sklearn import metrics
def scoring(y_true, y_pred):
r2 = round(metrics.r2_score(y_true, y_pred) * 100, 3)
# mae = round(metrics.mean_absolute_error(y_true, y_pred),3)
corr = round(np.corrcoef(y_true, y_pred)[0, 1], 3)
mape = round(
metrics.mean_absolute_percentage_error(y_true, y_pred) * 100, 3)
rmse = round(metrics.mean_squared_error(y_true, y_pred, squared=False), 3)
df = pd.DataFrame({
'R2': r2,
"Corr": corr,
"RMSE": rmse,
"MAPE": mape
},
index=[0])
return df
Validation Prediction 결과 에서 10개의 Store, 50개의 Item 중 몇개만 실제값과 예측값을 그래프로 그려보면 다음과 같다.
def abline(slope, intercept):
"""Plot a line from slope and intercept"""
axes = plt.gca()
x_vals = np.array(axes.get_xlim())
y_vals = intercept + slope * x_vals
plt.plot(x_vals, y_vals, '--')
def MinMax(y_true, y_pred, m="min") :
if(m == "min") :
return min(min(y_true),min(y_pred)) -2
else :
return max(max(y_true),max(y_pred)) +2
def myGraph(temp, title) :
fig, axs = plt.subplots(1,2,figsize=(20,5), gridspec_kw={'width_ratios': [2.5, 1]})
axs[0].plot(temp.date, temp.y_true, label = "Original")
axs[0].plot(temp.date, temp.y_pred, label = " Predicted")
axs[0].legend(loc='upper right')
axs[0].title.set_text(title)
axs[0].set_xlabel("Date")
axs[0].set_ylabel("Sales")
axs[1].plot(temp.y_true,temp.y_pred,'.')
plt.xlim(MinMax(temp.y_true,temp.y_pred),MinMax(temp.y_true,temp.y_pred,"max"))
plt.ylim(MinMax(temp.y_true,temp.y_pred),MinMax(temp.y_true,temp.y_pred,"max"))
abline(1,0)
plt.title(title)
plt.xlabel("Original")
plt.ylabel("Predicted")


7. CNN
CNN 아키텍처로 시계열 분석을 하기 위해 Input Data의 Shape을 3차원으로 변형해준다.
X_train_series = X_train.values.reshape((X_train.shape[0], X_train.shape[1], 1))
X_valid_series = X_valid.values.reshape((X_valid.shape[0], X_valid.shape[1], 1))
모델 아키텍처는 다음과 같다.
model_cnn = Sequential()
model_cnn.add(Conv1D(filters=64, kernel_size=2, activation='relu', input_shape=(X_train_series.shape[1], X_train_series.shape[2])))
model_cnn.add(MaxPooling1D(pool_size=2))
model_cnn.add(Flatten())
model_cnn.add(Dense(50, activation='relu'))
model_cnn.add(Dense(1))
model_cnn.compile(loss='mse', optimizer=adam)
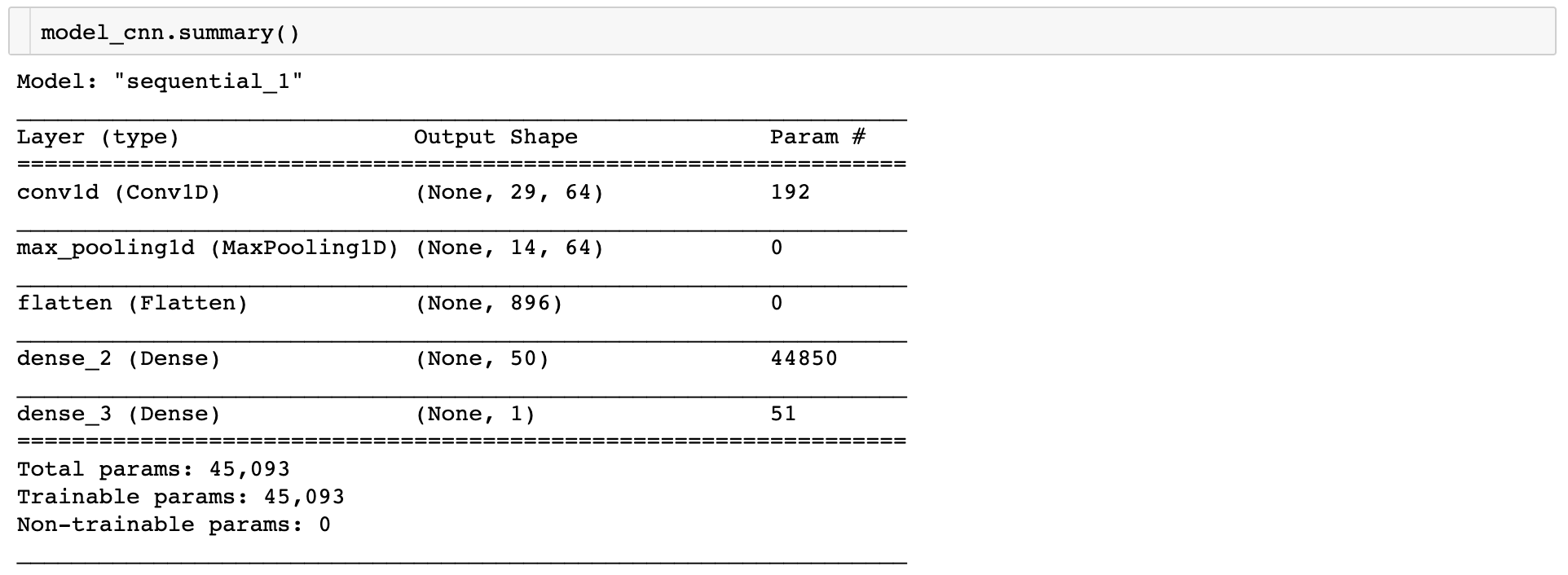
CNN 2Dimension output shape은 (Batch_size, width, height, depth)로 총 4차원으로 구성되어있다.
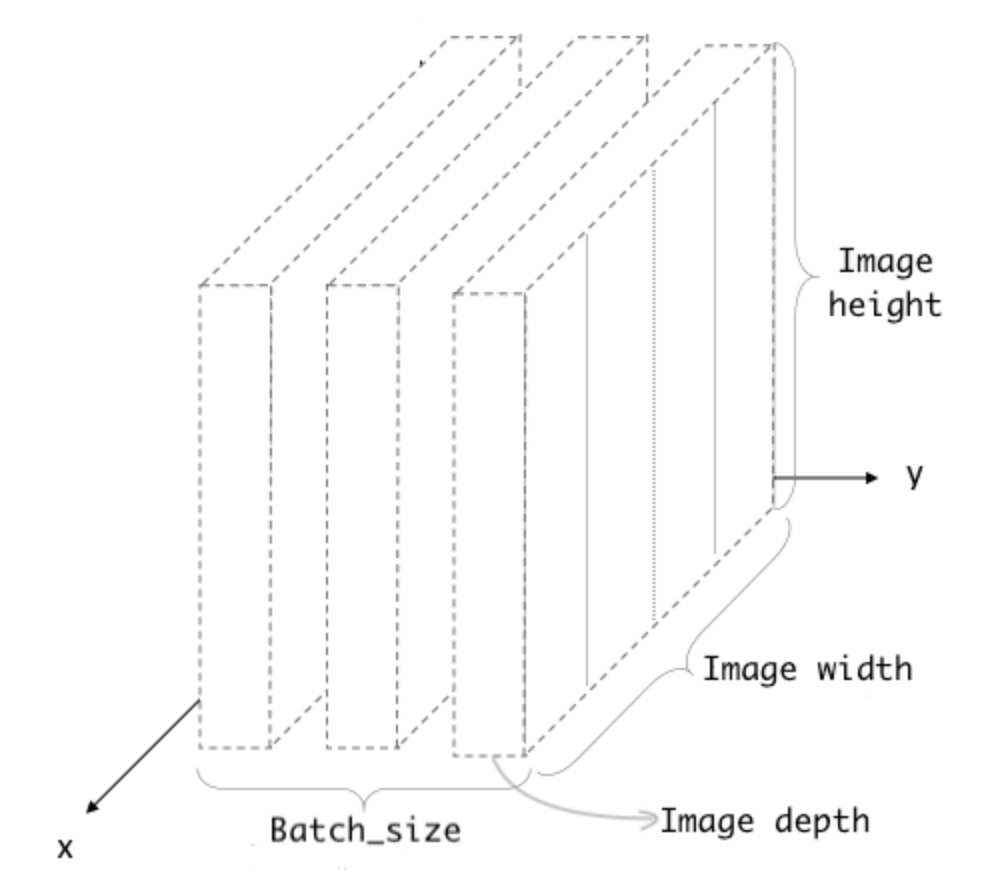
Batch Size를 모델 쌓을 때 넣어주는게 아니라, fitting할 때 파라미터로 전달하는 경우에는 아직 모르기 때문에 None으로 표시되기도 한다.
depth는 color 이미지에서 rgb라고 생각하면 쉽다. r, g, b 각각 한 장씩 총 3장이므로 컬러 이미지에서 input shape에 depth는 3이 된다.
Convolution filter를 통과 한 경우 output에서 depth는 filter 개수가 된다.
즉, 위 아키텍처에서 filters=64로 지정해주었으므로 output shape에 마지막 값이 64인 것이다.
Sales 데이터는 2차원이아니라 1차원이므로 width 없이 height 30, depth 1을 input shape으로 넣어주었다.
(참고) 2D Convolution VS 1D Convolution
2D Convolution
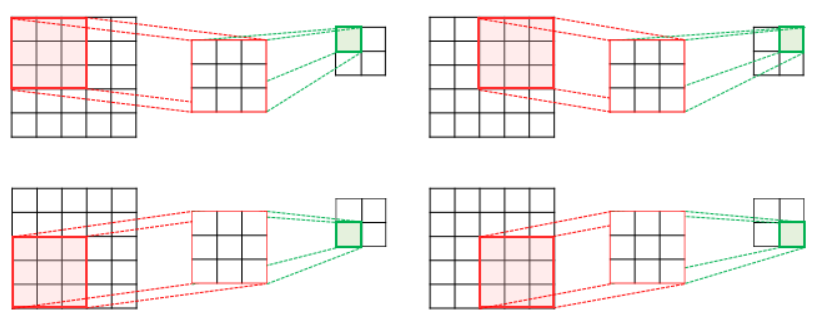
1D Convolution
이제 학습하고, 예측한다.
cnn_history = model_cnn.fit(X_train_series, Y_train, validation_data=(X_valid_series, Y_valid), epochs=epochs, verbose=2)cnn_train_pred = model_cnn.predict(X_train_series)
cnn_valid_pred = model_cnn.predict(X_valid_series)
Y_train_ = pd.DataFrame({'y_true': Y_train, 'y_pred': cnn_train_pred.reshape(cnn_train_pred.shape[0],)}).set_index(X_train.index).sort_index()
Y_train_ = pd.merge(Y_train_, train_gp,
left_index=True, right_index=True,
how='left')
Y_valid_ = pd.DataFrame({'y_true': Y_valid, 'y_pred': cnn_valid_pred.reshape(cnn_valid_pred.shape[0],)}).set_index(X_valid.index).sort_index()
Y_valid_ = pd.merge(Y_valid_, train_gp,
left_index=True, right_index=True,
how='left')
Train 성능과 Validation 성능은 다음과 같다.

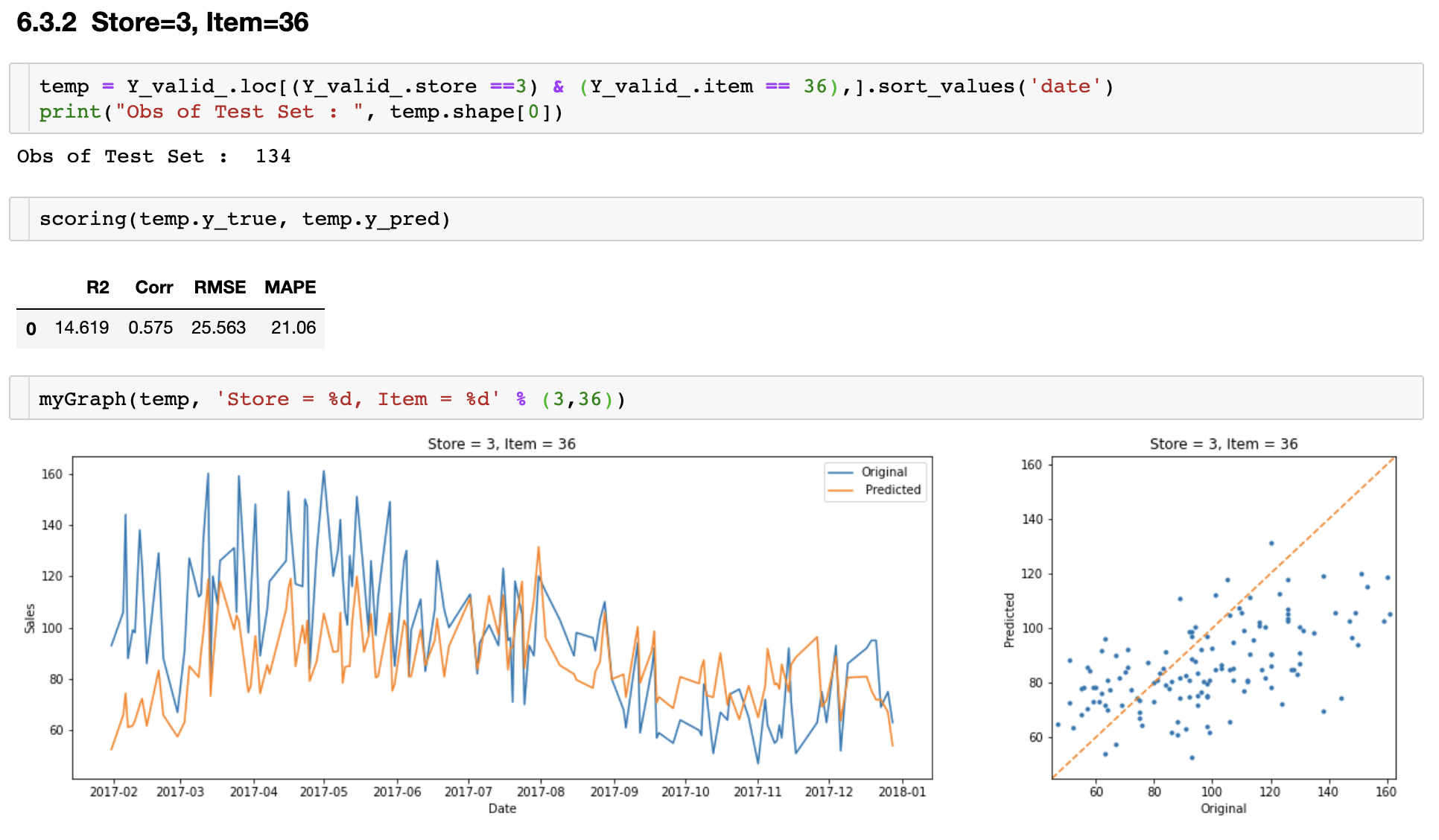
역시 Store와 Item 별로 몇개만 실제값과 예측값을 비교하여 그려보면 다음과 같다.

8. LSTM
다음으로 LSTM으로 시계열 분석하는 코드이다.
모델 아키텍처는 다음과 같다.
model_lstm = Sequential()
model_lstm.add(LSTM(50, activation='relu', input_shape=(X_train_series.shape[1], X_train_series.shape[2])))
model_lstm.add(Dense(1))
model_lstm.compile(loss='mse', optimizer=adam)
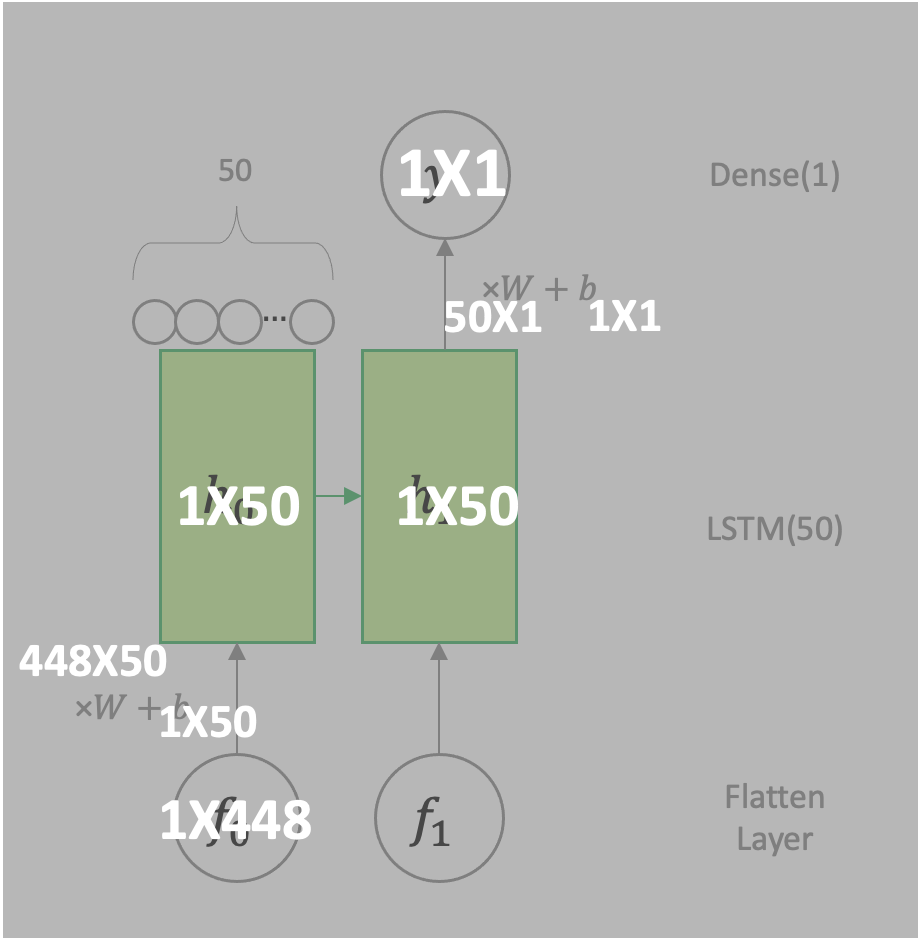
이를 그림으로 도식화해보면 다음과 같다.

각 노드의 Dimension을 도식화해보면 다음과 같다.
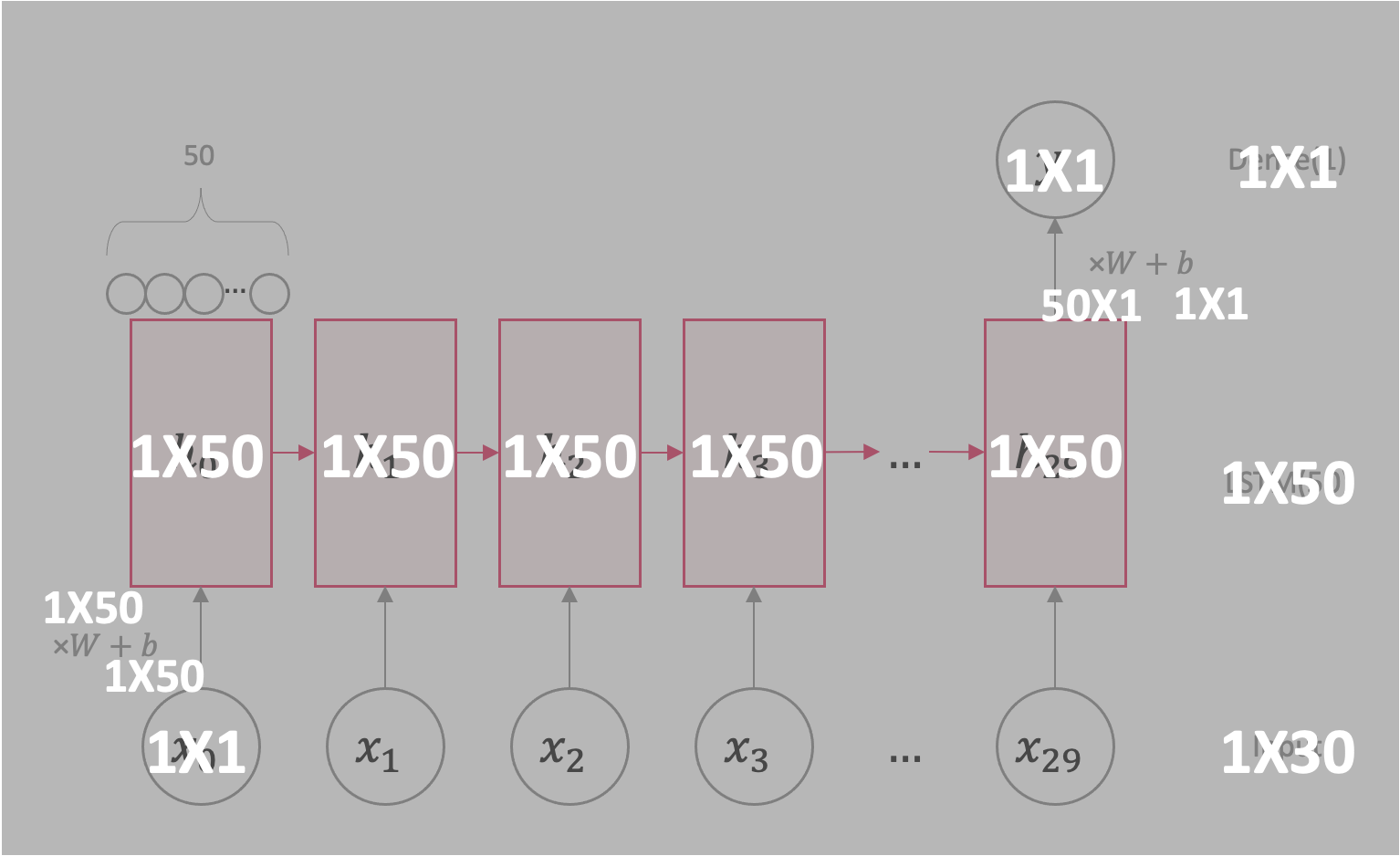
(1X1) Dimesion인 \(x_0\)에 (1X50)인 Weight를 곱해주고, Bias를 더해 (1X50)인 \(h_0\)가 되고,
(1X1) Dimesion인 \(x_1\)에 (1X50)인 Weight를 곱해주고, Bias를 더해 후 (1X50)인 \(h_0\)를 합한 \(h_1\)이 되고
...
(1X50)인 \(h_{29}\)에 (50X1)인 Weight를 곱하고 (1X1)인 Bias를 더해 (1X1)인 최종 Output이 된다.
참고로, LSTM은 Dense와 달리 셀 안에 단기 기억을 담당하는 부분과 장기 기억을 담당하는 부분 등 더 복잡하게 이루어져 있어, 필요한 Parameter 개수가 더 많다.(Param # 이 10,000개가 넘는 이유)
이를 학습하고, 예측한다.
lstm_history = model_lstm.fit(X_train_series, Y_train, validation_data=(X_valid_series, Y_valid), epochs=30, verbose=2)
(다른 알고리즘들은 모두 40 epoch 학습했지만, LSTM은 추후 epoch에 따른 Loss를 확인했을 때 30이 넘어가면 오히려 증가하는 현상을 보여, 30 epoch만 학습했다.)
lstm_train_pred = model_lstm.predict(X_train_series)
lstm_valid_pred = model_lstm.predict(X_valid_series)
Y_train_ = pd.DataFrame({'y_true': Y_train, 'y_pred': lstm_train_pred.reshape(lstm_train_pred.shape[0],)}).set_index(X_train.index).sort_index()
Y_train_ = pd.merge(Y_train_, train_gp,
left_index=True, right_index=True,
how='left')
Y_valid_ = pd.DataFrame({'y_true': Y_valid, 'y_pred': lstm_valid_pred.reshape(lstm_valid_pred.shape[0],)}).set_index(X_valid.index).sort_index()
Y_valid_ = pd.merge(Y_valid_, train_gp,
left_index=True, right_index=True,
how='left')
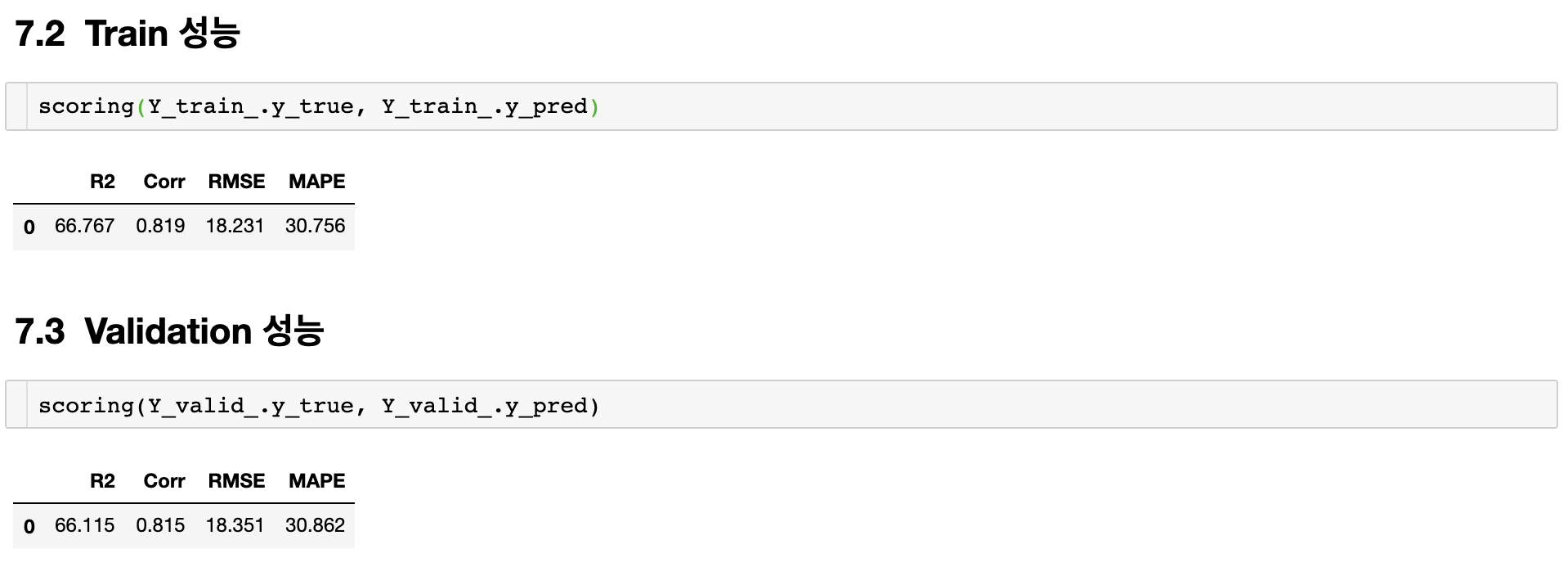
성능은 다음과 같다.


9. CNN + LSTM
마지막으로, 한 모델에 CNN과 LSTM을 둘 다 사용해 시계열 데이터를 분석하는 코드이다.
데이터 shape은 4차원으로 바꾸어 주었다.
subsequences = 2
timesteps = X_train_series.shape[1]//subsequences
X_train_series_sub = X_train_series.reshape((X_train_series.shape[0], subsequences, timesteps, 1))
X_valid_series_sub = X_valid_series.reshape((X_valid_series.shape[0], subsequences, timesteps, 1))

이렇게 3차원 데이터를 4차원으로 바꿔준 이유는 Dimensional Sentiment Analysis Using a Regional CNN-LSTM Model 논문에 잘 도식화 되어 있다.

LSTM은 Time Stamp에 따라 Input이 각각 들어와야 하기 때문에 2개로 나눈 것이다.
바꾸지 않았다면 즉, 1X30 형태로 Input에 넣어줬다면 다음과 같은 아키텍쳐가 나오게 된다.

2X15 형태로 바꿔주었기 때문에 다음과 같은 형태의 아키택쳐가 나올 수 있다.
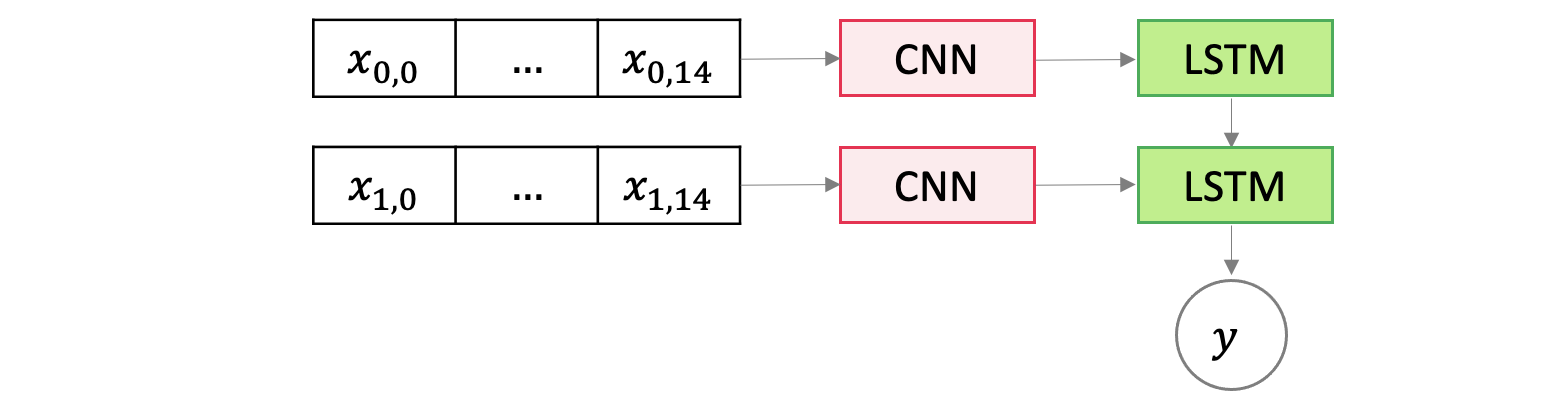
모델 아키텍처는 다음과 같다.
model_cnn_lstm = Sequential()
model_cnn_lstm.add(TimeDistributed(Conv1D(filters=64, kernel_size=1, activation='relu'), input_shape=(None, X_train_series_sub.shape[2], X_train_series_sub.shape[3])))
model_cnn_lstm.add(TimeDistributed(MaxPooling1D(pool_size=2)))
model_cnn_lstm.add(TimeDistributed(Flatten()))
model_cnn_lstm.add(LSTM(50, activation='relu'))
model_cnn_lstm.add(Dense(1))
model_cnn_lstm.compile(loss='mse', optimizer=adam)

이를 그림으로 도식화하면 다음과 같다.
첫 번째 Convolution Layer는 heigth 15, depth 1인 input에 size가 1인 Convolution Filter를 64개 적용해
15X64인 output이 나온다.

두 번째 MaxPooling Layer는 size가 2 이므로 15였던 height가 7이된다.

Flatten으로 한 줄로 펴주어 7*64 = 448이 나오고, 이 layer의 결과를 f라 표현하면, LSTM(50), Dense(1) 은 다음과 같다.
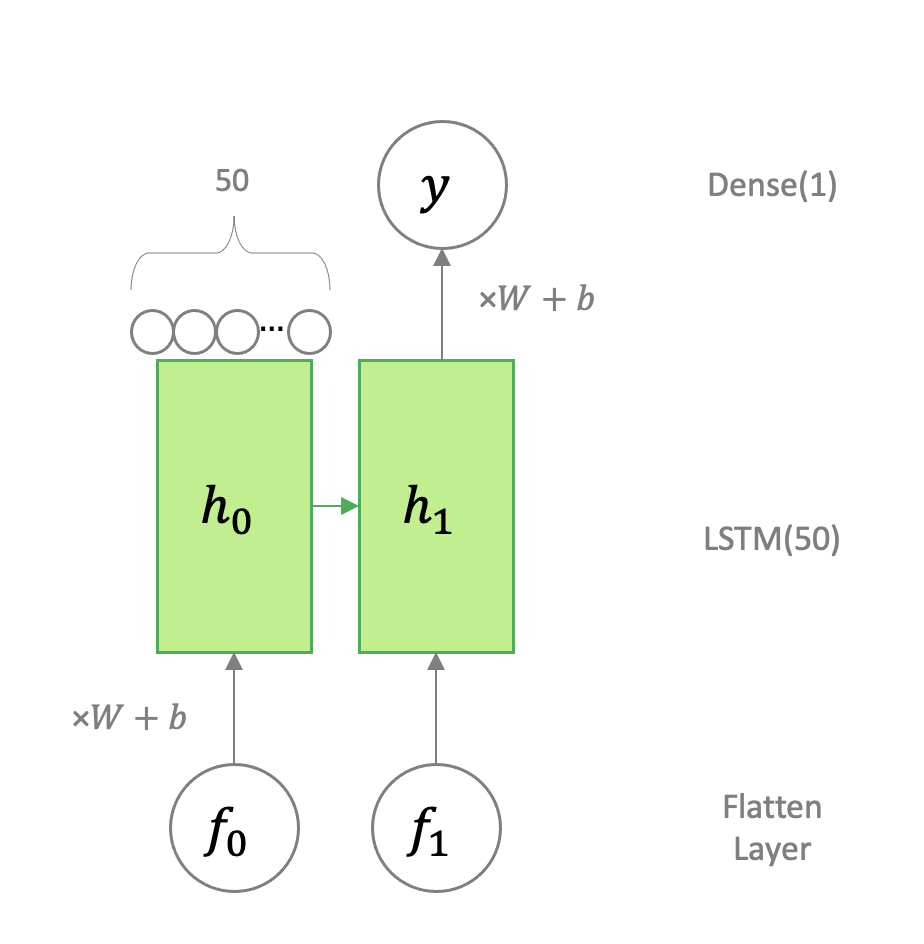
(Train Set의 subsequence가 2임을 고려하여 2개의 input으로 도식화하였다.)
flatten layer의 뉴런 수가 448개 이므로 이 Dimension을 다시 도식화 하면 다음과 같다.
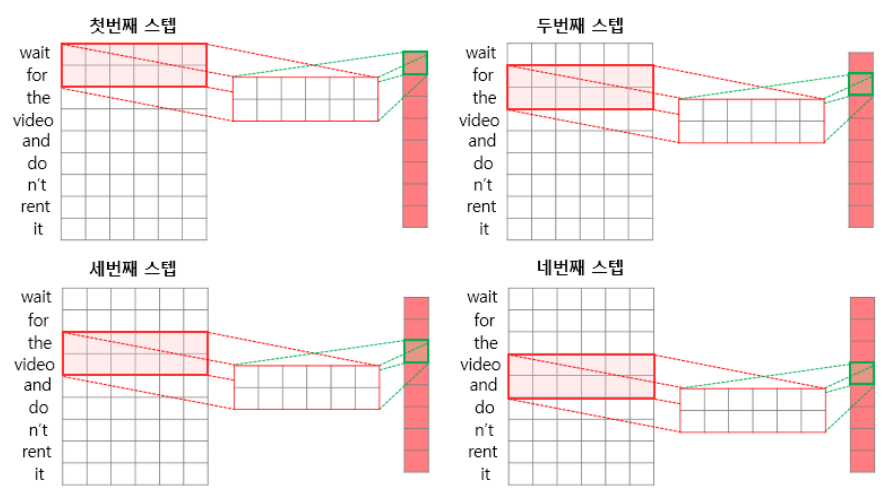
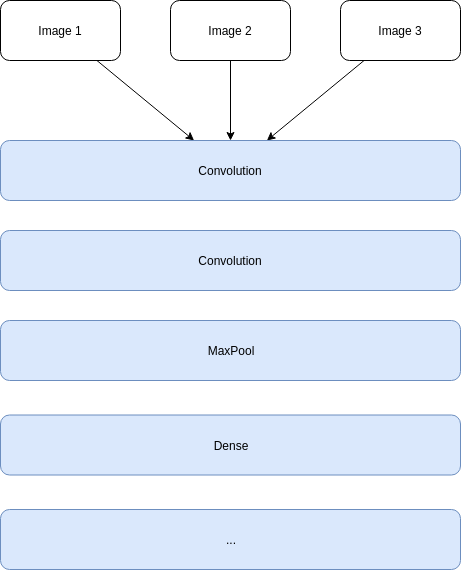
Model을 쌓을 때 Convolution 쪽에 TimeDistributed 라는 걸로 쌓여 있는 걸 볼 수 있다.
이 코드를 써주지 않으면 다음과 같이 time step이 나뉘지 않고 하나의 convolution filter로 학습이 된다.
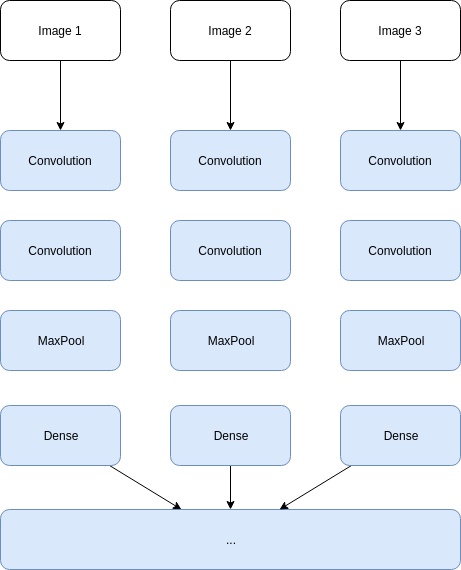
TimeDistributed를 써주어야 다음과 같이 input별로 각각의 convolution filter를 적용해 이후 LSTM과 결합할 수 있다.
이를 학습하고, 예측한다.
cnn_lstm_history = model_cnn_lstm.fit(X_train_series_sub, Y_train, validation_data=(X_valid_series_sub, Y_valid), epochs=epochs, verbose=2)cnn_lstm_train_pred = model_cnn_lstm.predict(X_train_series_sub)
cnn_lstm_valid_pred = model_cnn_lstm.predict(X_valid_series_sub)
Y_train_ = pd.DataFrame({'y_true': Y_train, 'y_pred': cnn_lstm_train_pred.reshape(cnn_lstm_train_pred.shape[0],)}).set_index(X_train.index).sort_index()
Y_train_ = pd.merge(Y_train_, train_gp,
left_index=True, right_index=True,
how='left')
Y_valid_ = pd.DataFrame({'y_true': Y_valid, 'y_pred': cnn_lstm_valid_pred.reshape(cnn_lstm_valid_pred.shape[0],)}).set_index(X_valid.index).sort_index()
Y_valid_ = pd.merge(Y_valid_, train_gp,
left_index=True, right_index=True,
how='left')


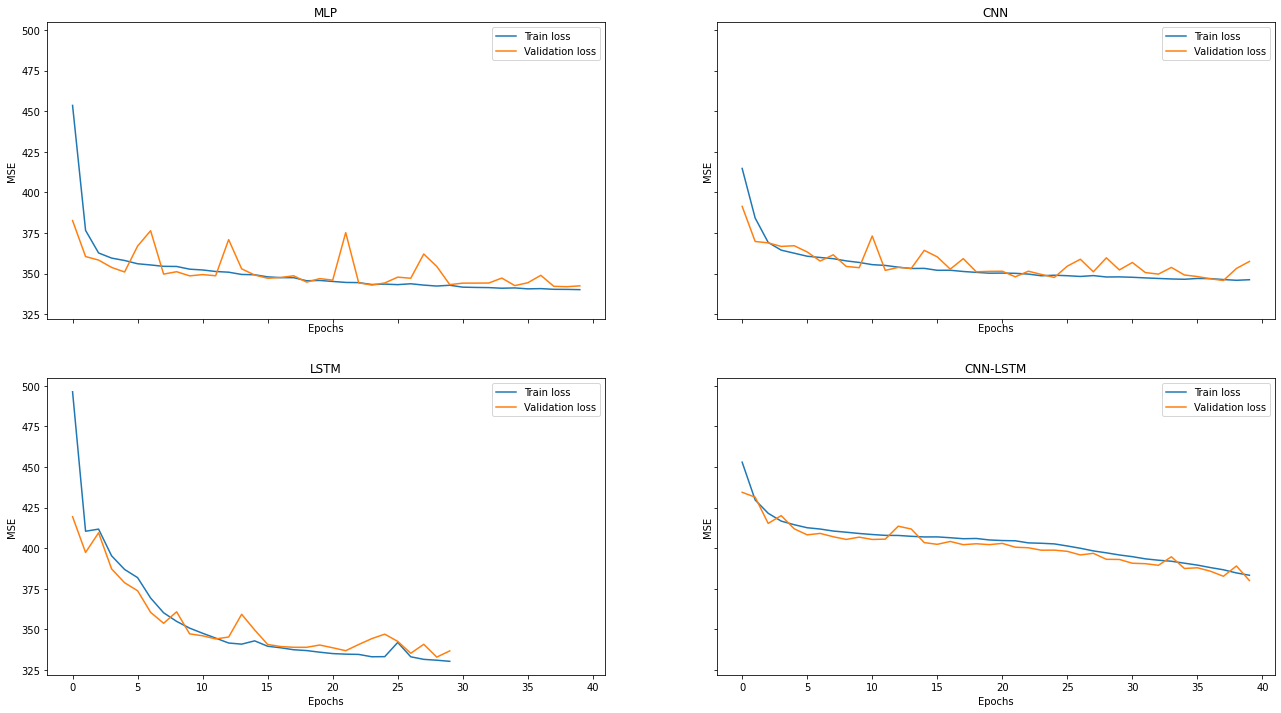
참고로 각 모델별 epoch에 따른 Loss(MSE)는 다음과 같다.
fig, axes = plt.subplots(2, 2, sharex=True, sharey=True,figsize=(22,12))
ax1 = axes[0,0]
ax2 = axes[0,1]
ax3 = axes[1,0]
ax4 = axes[1,1]
ax1.plot(mlp_history.history['loss'], label='Train loss')
ax1.plot(mlp_history.history['val_loss'], label='Validation loss')
ax1.legend(loc='best')
ax1.set_title('MLP')
ax1.set_xlabel('Epochs')
ax1.set_ylabel('MSE')
ax2.plot(cnn_history.history['loss'], label='Train loss')
ax2.plot(cnn_history.history['val_loss'], label='Validation loss')
ax2.legend(loc='best')
ax2.set_title('CNN')
ax2.set_xlabel('Epochs')
ax2.set_ylabel('MSE')
ax3.plot(lstm_history.history['loss'], label='Train loss')
ax3.plot(lstm_history.history['val_loss'], label='Validation loss')
ax3.legend(loc='best')
ax3.set_title('LSTM')
ax3.set_xlabel('Epochs')
ax3.set_ylabel('MSE')
ax4.plot(cnn_lstm_history.history['loss'], label='Train loss')
ax4.plot(cnn_lstm_history.history['val_loss'], label='Validation loss')
ax4.legend(loc='best')
ax4.set_title('CNN-LSTM')
ax4.set_xlabel('Epochs')
ax4.set_ylabel('MSE')
plt.show()
'AI > 시계열자료 분석' 카테고리의 다른 글
| [Python] 날씨 시계열 데이터(Kaggle)로 ARIMA 적용하기 (16) | 2021.05.25 |
|---|---|
| ARIMA란? :: ARIMA 분석기법, AR, MA, ACF, PACF, 정상성이란? (6) | 2021.05.24 |
| 시계열 분해란?(Time Series Decomposition) :: 시계열 분석이란? 시계열 데이터란? 추세(Trend), 순환(Cycle), 계절성(Seasonal), 불규칙 요소(Random, Residual) (0) | 2021.05.24 |
| [시계열 자료 분석] R에서 AirPassengers 데이터 선형계절추세모형 적합시키기 (0) | 2019.10.31 |
| [R] stl() 이란? :: stl parameter :: stl s.window (0) | 2019.10.29 |