시계열 데이터란?
시간에 순차적으로 관측한 값들의 집합이며, 예측 모델에서 시간을 변수로 사용하는 특징이 있다.
시계열 데이터 분석이란?
과거 데이터의 패턴을 분석하여 미래의 값을 예측하는 방법으로, 과거의 패턴이 미래에도 지속된다는 데이터의 안정성이 기본적인 가정으로 필요하다.
시계열 분해법이란? What is Time Series Decomposition?
시계열 데이터를 추세/순환/계절/불규칙 요소로 분해하는 기법이다.
추세(Trend)란?
데이터가 장기적으로 증가하거나 감소하는 것이며, 추세가 꼭 선형적일 필요는 없다.
순환(Cycle)이란?
경기변동과 같이 정치, 경제, 사회적 요인에 의한 변화로, 일정 주기가 없으며 장기적인 변화 현상이다.
계절성(Seasoanl)이란?
주, 월, 분기, 반기 단위 등 특정 시간의 주기로 나타나는 패턴이다.
불규칙요소(Random, Residual)란?
설명될 수 없는 요인 또는 돌발적인 요인에 의하여 일어나는 변화로, 예측 불가능한 임이의 변동을 의미한다.
분해법에서는 원래 데이터에서 추세, 순환, 계절성은 뺀 나머지를 불규칙 요소라 한다.
즉, 시계열 데이터는 추세, 순환, 계절성, 불규칙요소로 이루어져 있으며 이를 식으로 나타내면 다음과 같다.
1. 덧셈 분해(additive decomposition)
$$ y_t = S_t+T_t+R_t $$
여기서 \(y_t\) 는 데이터이고, \(t\)는 시점, \(S_t\)는 계절 성분, \(T_t\)는 추세 및 순환 성분, \(R_t\)는 불규칙 요소를 의미한다.
2. 곱셈 분해(multiplicative decomposition)
덧셈 대신 곱셈으로 분해하는 경우도 존재한다. 이 때, 식은 다음과 같다.
$$ y_t = S_t*T_t*R_t $$
단, multiplicative 모델을 활용하려면 데이터에 0이 존재해서는 안된다.
덧셈 분해와 곱셈 분해의 차이점은
덧셈 분해는 Trend와 Seasonal이 별개이고, 곱셈 분해는 Trend에 따라 Seasonal이 변화한다고 보면 된다.
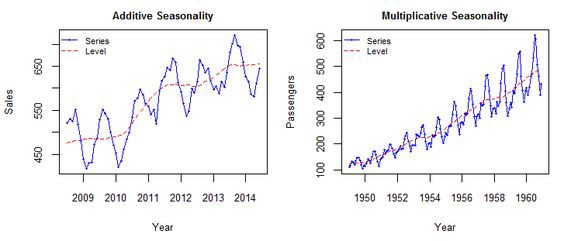
위 그림에 첫 번째 예시는 시간에 지남에 따라(Trend가 변화함에 따라) 변동폭이 일정하지만, 두 번째 그림은 Trend가 상승함에 따라 변동폭 역시 증가하고 있다. 즉, 첫 번째 예시는 Additive가 적절하고, 두 번째 예시는 Multiplicative가 적절하다.
다음 글에서 설명하겠지만, ARIMA 모형은 정상성을 가정하고 있다.
시간에 따라 변동폭이 일정하지 않을 경우에는 정상성 가정을 만족하지 못해 로그 변환을 해 주는데,
즉, \(y_t = S_t*T_t*R_t\)의 곱셈 분해는 로그 변환으로 \(logy_t=logS_t+logT_t+logR_t\)과 같이 덧셈 분해와 같아진다.
이는 R 또는 Python에서 코드 한 줄로 구현할 수 있는데,
R에서는 stats 패키지의 decompose(), Python에서는 statsmodels.tsa.seasonal 패키지의 seasonal_decompose() 함수를 활용하면 된다.
decompose()는 type에 "additive" 또는 "multiplicative"로 덧셈 분해와 곱셈 분해를 구분하여 넣어주면 되고,
seasonal_decompose()는 model="additive" or "multiplicative"로 구분해서 넣어주면 된다.
예시는 다음과 같다.
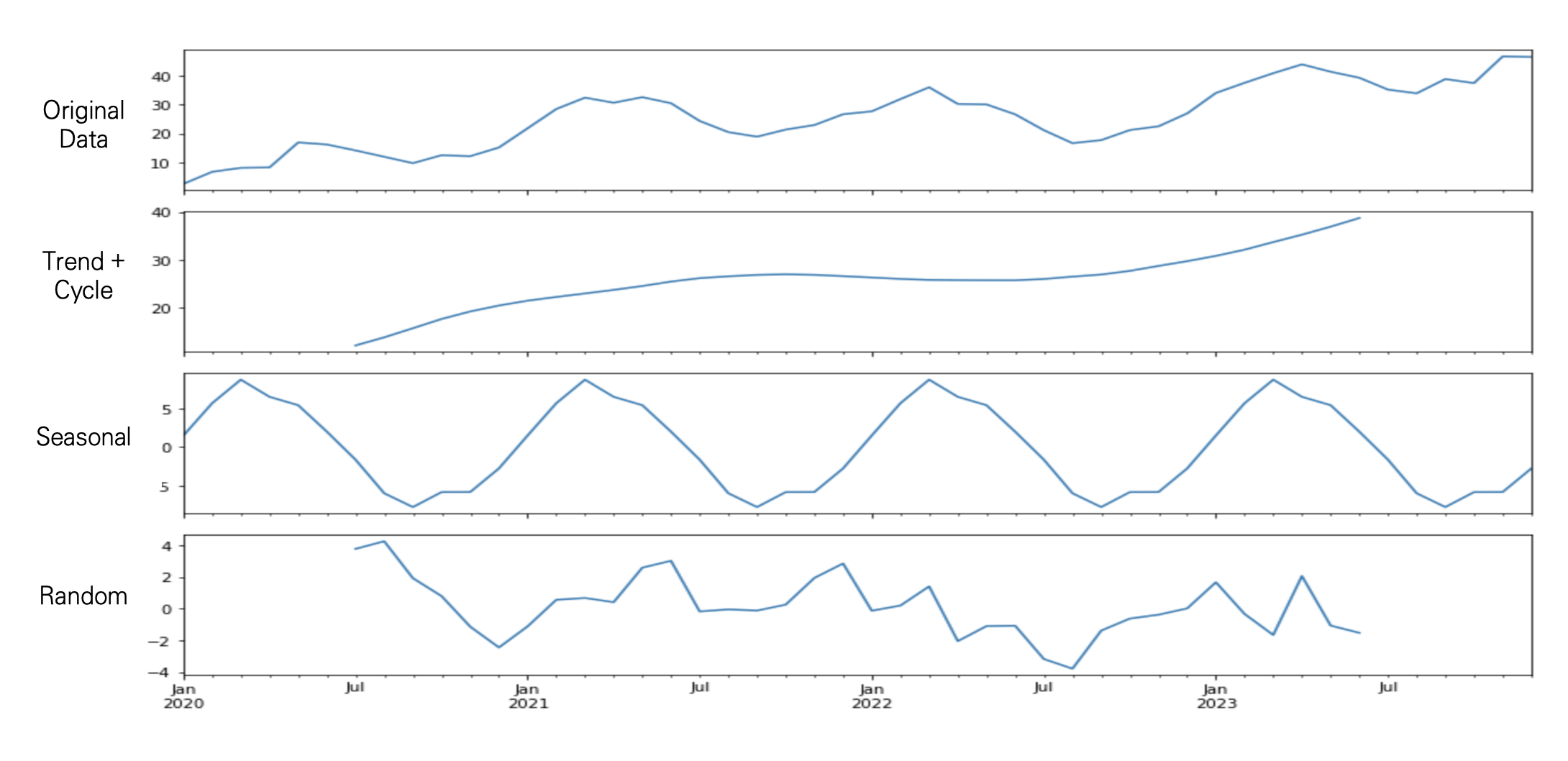
가장 위의 raw 데이터를 Trend, Cycle, Seasonal, Random 요소로 분해한 결과이다.
점진적으로 증가하는 추세를 보이며, 약간의 계절성도 가지고 있음을 알 수 있다.
Raw 데이터를 각각의 패턴으로 해석하는 예시는 다음과 같다.

미국 단독 주택 거래량 같은 경우, 전체 기간에 걸쳐 분명한 추세가 있지는 않지만, 매년 강한 계절성과 약 6~10년 주기의 패턴이 존재한다.
미국 재무부 단기 증권 계약의 경우, 점진적으로 하향하는 추세가 보인다.
호주 분기별 전력 생산의 경우, 강항 계절성과 증가 추세가 보인다.
구글 주식 종가 기준 일별 변동은 추세, 계절성 및 주기적인 패턴이 보이지 않는다.
이러한 패턴에 따라 분석 기법이 달라지기 때문에, 알고리즘에 fitting 하기에 앞 서, EDA과정을 거쳐 데이터의 특성을 파악해야 한다.
참고 및 출처
https://otexts.com/fppkr/index.html
Forecasting: Principles and Practice (2nd ed)
2nd edition
Otexts.com
'AI > 시계열자료 분석' 카테고리의 다른 글
| Deep Learning for Time Series Forecasting (kaggle 코드 리뷰) (30) | 2021.05.27 |
|---|---|
| [Python] 날씨 시계열 데이터(Kaggle)로 ARIMA 적용하기 (16) | 2021.05.25 |
| ARIMA란? :: ARIMA 분석기법, AR, MA, ACF, PACF, 정상성이란? (6) | 2021.05.24 |
| [시계열 자료 분석] R에서 AirPassengers 데이터 선형계절추세모형 적합시키기 (0) | 2019.10.31 |
| [R] stl() 이란? :: stl parameter :: stl s.window (0) | 2019.10.29 |