슈퍼짱짱

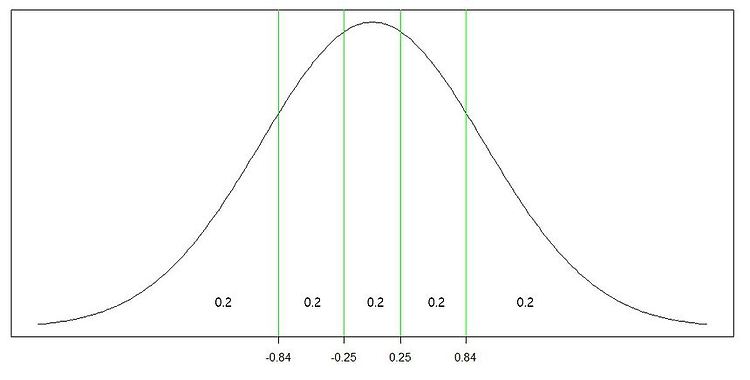
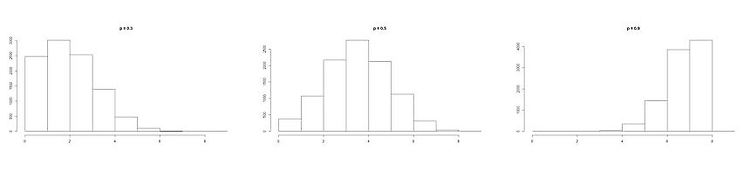
정규확률그림이란? What is Q-Q plot? 많은 경우에 통계적인 절차나 분석 등에서 모집단의 분포가 정규분포를 따른 다는 가정을 하고 있다. 그렇다면 표본을 추출했을 때 이러한 정규모집단의 가정을 조사하는 방법은 어떤 것이 있을까? 그 방법 중 하나가 바로 정규확률그림으로 확인하는 것이다.정규점수그림(normal scores plot) 또는 정규확률그림(normal probability plot)이라 하는데 정규확률그림이라는 용어를 더 많이 쓴다. 이 때, 정규점수(normal scores)란 표준정규분포(mean=0,sd=1)에서의 이상적인 표본을 말한다. 즉, 표준정규분포의 확률밀도함수를 등확률 구간으로 나누어 주는 경계값(z값)을 의미한다. 분위수를 생각해보면 쉽다. n분위수에 해당하는 z값..

이전 포스팅에서 베르누이 시행에 대해 알아보았다. 본 포스팅에서는 이항분포에 대해 알아보겠다. 이항분포란? 성공할 확률이 p인 베르누이 시행을 n번 반복할 때에 일어나는 성공의 횟수를 X라 하면, 이 확률변수 X의 확률변수를 모수가 (n, p)인 이항분포라 한다. 즉, 쉽게 생각해 경우의 수가 2개뿐인 실험 1번 시행 - 베르누이/ 베르누이를 n번 시행 - 이항분포 이항분포(binomial distribution) n : 베르누이 시행의 반복 횟수 p : 각 시행에서 성공할 확률, P(S)X : n번 시행 중 성공의 횟수 이와 같이 정의된 확률변수 X를 이항 확률변수라 하고 그 분포를 이항분포라 한다. X~Bin(n,p)로 표현하기도 한다. 이항 확률변수 X가 취하는 값의 범위는 0, 1, 2, ...,..

기초통계 - 이항분포와 관련있는 베르누이 두 그룹으로 나누어져 있는 모집안에서 표본을 추출하는 경우, 각 단계의 추출은 두 가지의 결론만을 갖게된다. 동전던지기가 그 예이다. 동전을 던졌을 때 그 결과는 앞면, 뒷면으로 두 가지만 나타난다. 이런 경우 매번 반복되는 추출(실험)을 통계학용어로 시행(trial)이라 부르고, 두 개의 가능한 결과 중 하나는 성공(S, success), 다른 하나는 실패(F, failure)라 부르는데, 이는 시행 결과가 두 개뿐임을 의미하며 진짜 성공과 실패와는 부관하다. 보통 관심있는 결과를 성공이라 부른다. 이 '성공'과 '실패'로 나타나는 시행이 반복되면서 다음과 같은 조건이 만족되는 경우 이를 베르누이 시행이라 부른다. 베르누이 시행(Bernoulli trial) (..

상관계수란? 이전 포스팅에서 두 연속형 변수의 관계를 눈으로 확인하기 위한 산점도에 대해 알아보았다.산점도로부터 파악할 수 있는 관계는 객관성이 부족한 면이 있다. 예를 들어 동일한 크기의 좌표평면에서 좌표의 눈금을 변화시키면(변수의 측정 단위를 변화시키면) 두 변수의 관계가 다른 것처럼 보여질 수 있다. 따라서 좀 더 객관적으로 두 변수간의 관계를 알아볼 수 있는 상관계수에 대해 알아보겠다. 두 변수로 산점도를 그려보면 직선, 곡선 등 여러 형태를 가질 수 있는데, 여기서 가장 관심이 있는 경우는 직선의 형태이다. 산점도에서 점들이 얼마나 직선에 가까운가의 정도를 나타내는데 쓰이는 측도가 상관계수이다. 상관계수란? 두 변수 x,y 사이의 상관관계의 정도를 나타내는 수치 상관계수는 피어슨(Karl Pea..

두 연속형 변수의 요약 : 산점도 지난 포스팅에서 두 범주형 변수의 요약방법인 분할표에 대해 알아보았다.이번에는 두 연속형 변수의 관계를 알아보기 위한 첫 번째 단계인 산점도에 대해 알아보겠다. 두 연속형 변수 x와 y에 대해 1. 두 변수는 서로 관계가 있는가? 2. 있다면, 어떤 관계인가? 라는 질문을 할 수 있다.이 때, (x,y)에 대해 그림을 그려 그 관계를 눈으로 파악 할 수 있는데, 이 그림을 산점도라 한다. 산점도란? 변수 x를 수평축에 놓고 변수 y를 수직축에 놓은 후에 각 관측값의 짝을 좌표 위에 표시함으로써 얻게되는 그림 이렇게 그린 그림을 관측값들이 직선이나 곡선의 띠를 형성하고 있는지, 또는 특별한 경향 없이 무작위로 흩어져있는지 확인할 수 있다. 예)1990년도 국가별 국내총생산..

두 범주형 변수의 요약 : 분할표 분할표란? 두 변수에 대한 관측값을 요약하고 해석하는 방법 중 하나로, 두 변수가 모두 범주형에 속할 때, 도수분포표를 2차원으로 확장한 형태로 요약할 수 있다.한 변수에 대한 범주는 왼쪽에, 또 다른 변수에 대한 범주는 위쪽에 표시하고, 두 변수의 범주들이 교차하는 칸마다 각 변수의 범주를 동시에 갖는 관측값들의 수를 그 칸의 도수로 기록한다. 이렇게 도표로 요약된 자료를 분할표라 부른다. >>> 범주형자료란? 바로가기>>> 범주형자료 표현하는 방법 바로가기 예)새로이 제한된 어떤 정책에 대한 지지여부를 알아보기 위하여 400명을 임의로 추출하여 조사했다.표본으로 추출된 각 개인의 성별과 지지여부를 해당 범주에 따라 정리한 결과가 다음과 같다.  찬성 미결정 반대 합계..

소프트맥스란? What is softmax? softmax란? 신경망의 출력층에서 사용하는 활성화 함수로, 분류문제에 쓰이는 함수이다. * 회귀에서는 항등함수(identity function)을 사용한다. softmax의 식은 다음과 같다. 파이썬에서 소프트맥스 함수 구현하기 (softmax in python) 파이썬에서 seoftmax 함수는 다음과 같이 구현한다. 12345678import numpy as np def softmax(a) : exp_a = np.exp(a) sum_exp_a = np.sum(exp_a) y = exp_a / sum_exp_a return ycs 이를 한 줄씩 실행하면 다음과 같다. 1234a = np.array([0.3,2.9,4.0])exp_a = np.exp(a)s..

백준 9020 골드바흐의 추측 in python https://www.acmicpc.net/problem/9020 코드 12345678910111213141516171819202122# n이하의 숫자들 중 소수 찾기def prime_list(n): sieve = [True] * n m = int(n ** 0.5) for i in range(2, m + 1): if sieve[i] == True: for j in range(i+i, n, i): sieve[j] = False return [i for i in range(2, n) if sieve[i] == True] # n이하의 소수들 중 합이 ndef sosu(n): li=prime_list(n) idx = max([i for i in range(len(..

백준 3053 택시 기하학 in python 쉽게 풀어보기 코드 1234import mathr=int(input())print(r*r*math.pi)print(r*r*2)cs 코드설명 이 문제는 유클리드 기하학에서의 원과 택시 기하학에서의 원만 알면 쉬워진다. 즉, 유클리드 기하학에서의 원의 넓이은 원래 알던 식 그대로 pi*R^2 이고, 택시 기하학에서는 밑변의 길이와 높이가 R인 삼각형 네 개의 넓이를 구하면 된다.

백준 4153 직각삼각형 in python 쉽게 풀어보기 코드 1234567while 1: v = list(map(int, input().split())) m = max(v) if m == 0: break v.remove(m) if v[0]**2 + v[1] **2 == m**2 : print("right") else : print("wrong")cs