2020/04/21 - [통계 지식/Algorithm] - Decision Tree란? :: ID3 알고리즘, 엔트로피란?
Decision Tree란? :: ID3 알고리즘, 엔트로피란?
의사결정나무란? Decision Tree란? 의사결정 규칙을 나무구조로 나타내에 전체 데이터를 소집단으로 분류하거나 예측하는 분석기법 전체 데이터에서 마치 스무고개하듯이 질문하며 분류해나간다. 그 모양이 마치..
leedakyeong.tistory.com
2020/04/21 - [통계 지식/Algorithm] - 의사결정나무(Decision Tree) :: CART 알고리즘, 지니계수(Gini Index)란?
의사결정나무(Decision Tree) :: CART 알고리즘, 지니계수(Gini Index)란?
이전 포스팅에서 의사결정나무란 무엇인지, 어떤 기준으로 모델을 만들어가며 불순도가 무엇인지와 ID3 알고리즘에 대해 소개했다. 지난 포스팅 바로가기 https://leedakyeong.tistory.com/entry/Decision-Tree%EB..
leedakyeong.tistory.com
이전 포스트에서 의사결정나무의 개념과 대표 알고리즘 ID3, CART 에 대해 알아보았다.
지난 시간에는 독립변수가 범주형일 때만 다뤘다면, 이번에는 독립변수가 연속형일 때 어떻게 계산하는지 알아보겠다.
참고로 ID3 알고리즘은 독립변수가 범주형일 때만 가능하나, 연속형일 때도 가능하도록 발전한 알고리즘인 C4.5 가 있다. (불순도를 엔트로피로 계산한다.)
의사결정 나무 :: 독립변수가 연속형 일 때 Split 하는 방법
연속형 변수를 Split하는 방법은 크게 세 가지가 있다.
연속형 변수를 Split하는 방법
1. 전체 데이터를 모두 기준점으로 분할 후 불순도 계산
2. 중위수, 사분위수를 기준점으로
3. Label의 Class가 바뀌는 수를 기준점으로
위 세 방법 중 3번으로 설명하겠다.
12개 가정의 소득과 주택크기에 따른 잔디깎이 기계구입여부에 대한 데이터가 있다.
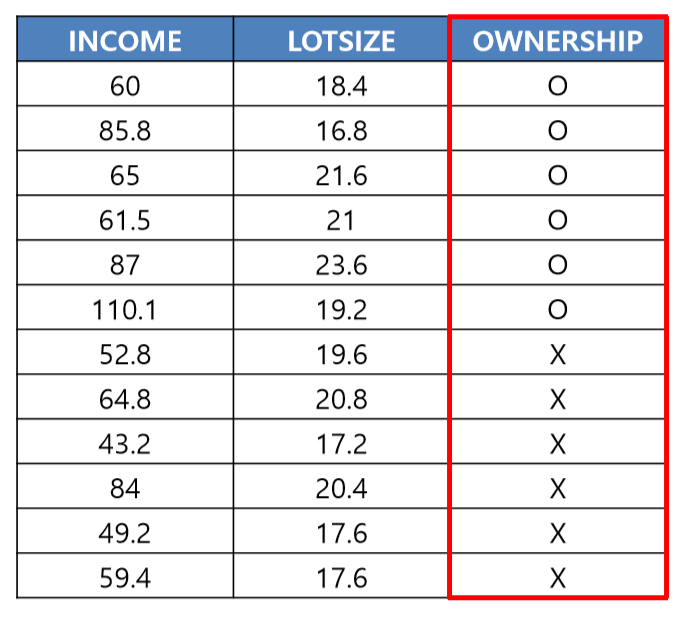
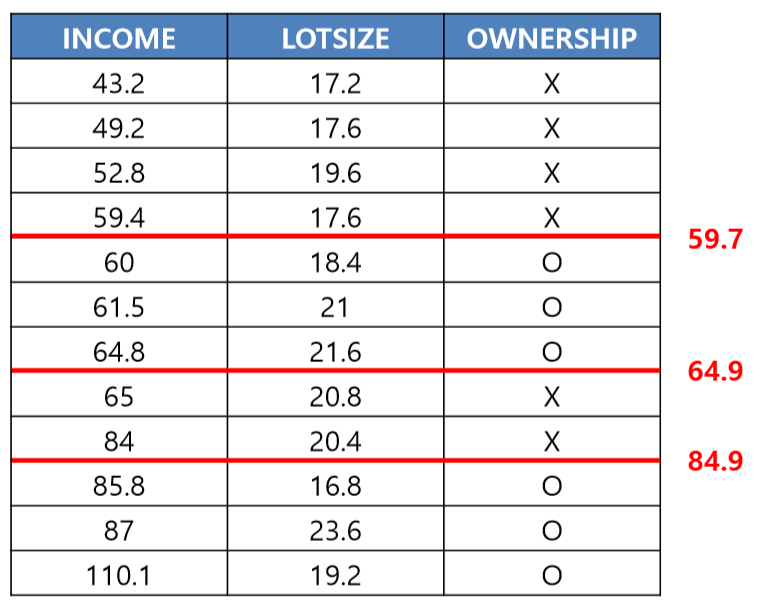
Approach 1) 각 속성(Features)에 대해 오름차순 정렬 (INCOME)

Approach 2) Label의 Class가 바뀌는 지점 찾기

Approach 3) 경계의 평균값을 기준값으로 잡기
LOTSIZE 도 똑같이 반복

Approach 4) 각 기준점에 대해 분할 후 Gini Index or Entropy 계산
이 예시에서는 지니계수로 계산했다.

분할 후 계산한 지니계수값이 가장 작은 income이 59.7보다 작을 때와 클 때는 첫 번째 기준점으로 분할한다.

이전 포스팅에서도 반복했듯이, 각 terminal node에 대해 위 계산을 반복해 tree를 키워나간다.
이렇게 계속 트리를 키워나가기만 한다면 과적합(overfitting)의 위험이 발생한다. 다음 포스팅에서는 이를 방지하기 위한 가지치기(Pruning)과 앙상블에 대해 소개하겠다.
'AI > Decision Tree Based Learning' 카테고리의 다른 글
| 의사결정나무(Decision Tree) :: 과적합(overfitting) 해결방법 :: 가지치기, 앙상블(Random Forest) (2) | 2020.04.21 |
|---|---|
| 의사결정나무(Decision Tree) :: CART 알고리즘, 지니계수(Gini Index)란? (2) | 2020.04.21 |
| Decision Tree란? :: ID3 알고리즘, 엔트로피란? (2) | 2020.04.21 |