RaPP(Novelty Detection with Reconstruction along Projection Pathway) 구현 :: Tensorflow, mnist

2020년 4월에 ICLR 개재된 RaPP를 Tensorflow로 구현해보았다.

 

논문 링크 : https://openreview.net/forum?id=HkgeGeBYDB 

RaPP: Novelty Detection with Reconstruction along Projection Pathway

참고 링크 : https://makinarocks.github.io/rapp/

RaPP - Novelty Detection with Reconstruction along Projection Pathway

참고 링크는 실제 논문 저자가 작성한 페이지이다. 논문에 다 담지 못한 추가 설명들도 적혀있다.

 

논문 링크에 따라가 보면 torch로 구현된 코드가 있기는 하나, 논문 작성용으로 만들어진 코드로, MNIST 뿐 아니라, MI-F, MI-V, EOPT, NASA 등 다양한 데이터에 적용하기 위해 복잡하게 구현이 되어있다.

따라서, 간단하게 MNIST에 적용하는 Tesorflow 코드로 재구현 해보았다.

---

RaPP에 대해 간단하게 설명하자면, Outlier Detection 보다는 Novelty Detection에 적합한 방법이다.

 

Outlier Detection VS Novelty Detection

 

 

Anomaly Detection의 대표적인 방법으로 Auto Encoder를 활용하여 Reconstrunction Error를 비교하는 방법이 있는데, 이를 확장한 방법이다. 

 

(참고) Anomaly Detection by Auto Encoder

2021.05.12 - [AI/Anomaly Detection] - Anomaly Detection by Auto Encoder

Anomaly Detection by Auto Encoder

 

RaPP의 기본 동작 원리는 다음과 같다.

 

 

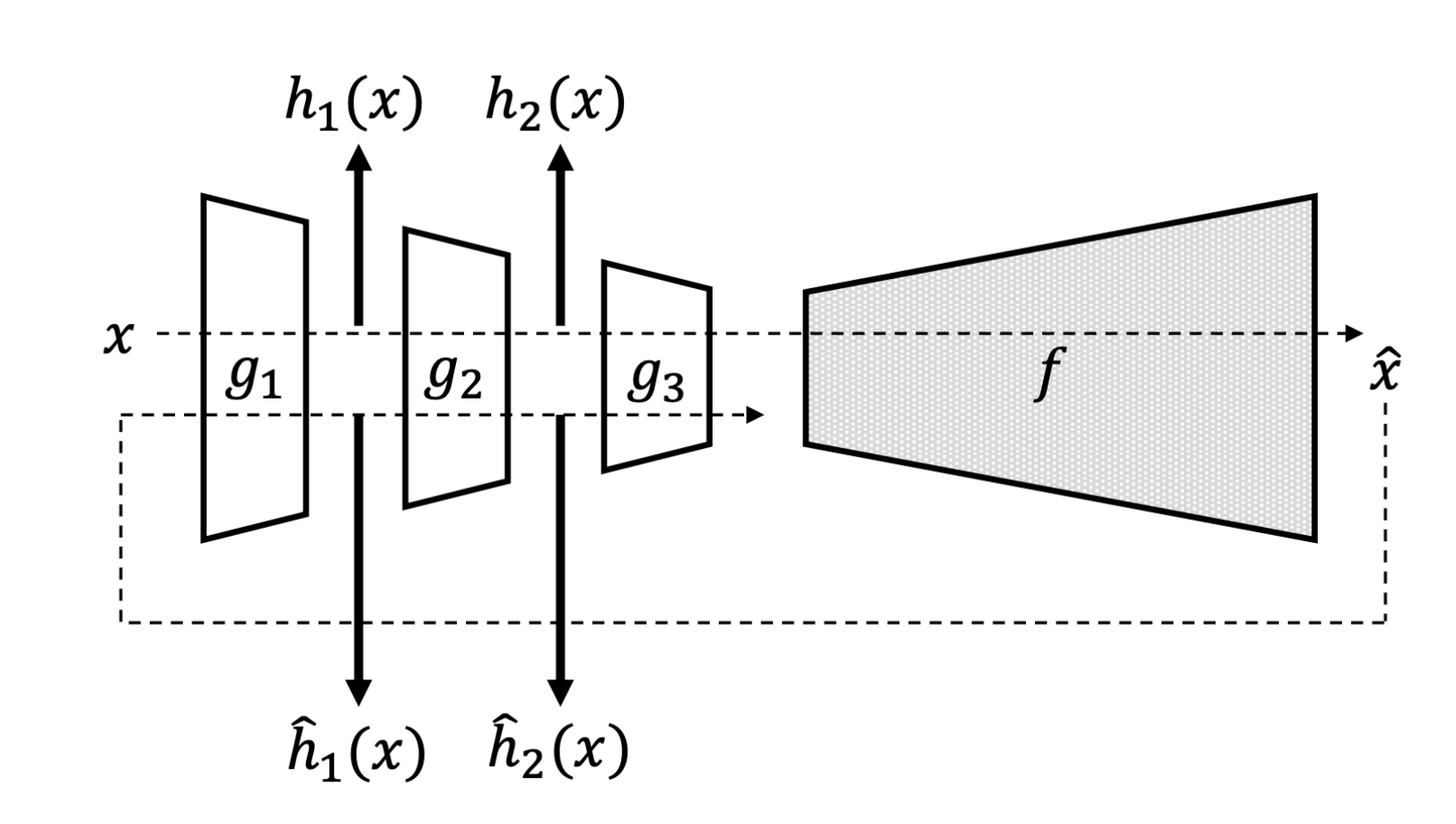
학습 할때부터 뭔가 처리하는건 아니고, 이미 학습된 AE에 Reconstruction Error만 새롭게 정의한다.

 

기존의 AE 방법은 input과 최종 output의 차이로만 Reconstruction Error를 정의하여 Abnormal과 Normal을 비교했다면, 

RaPP는 Encoder 부분의 모든 Layer를 활용하여 Reconstruction Error를 재정의한다.

 

먼저, raw input(\(x\))을 Auto Encoder에 통과시켜 각 Encoder Layer별 output(\(h_1(x), h_2(x), ...\))과 Decoder 까지 통과시킨 \(x^{'}\)를 얻고, 이 \(x^{'}\)를 다시 Auto Encoder에 통과시켜 역시 각 Encoder Layer별 output((\(\hat{h_1(x)}, \hat{h_2(x)}, ...\))을 계산한다. ( \(\hat{h_n(x)} = h_n(x^{'})\) )

이후 각 Enocder Layer별 \((h_n(x)\) - \(\hat{h_n(x)})^2\)을 쭉 한 줄로 concat 하여 Abnormal Score를 계산한다.

 

Concatenation

 

예를 들어, 8개 뉴런, 4개 뉴런, 2개 뉴런으로 이루어진 총 3 layer로 구성된 Enocder라 하자.

각각의 layer를 통과한 \((h_n(x)\) - \(\hat{h_n(x)})^2\)를 아래와 같이 쭉 한 줄로 concat하면 총 14(=8+4+2)개의 컬럼을 가진 1개 row가 생성된다. (입력 데이터 1개 당 1개 row 생성. -> n개 입력 시 n개 row 생성.)

 

 

---

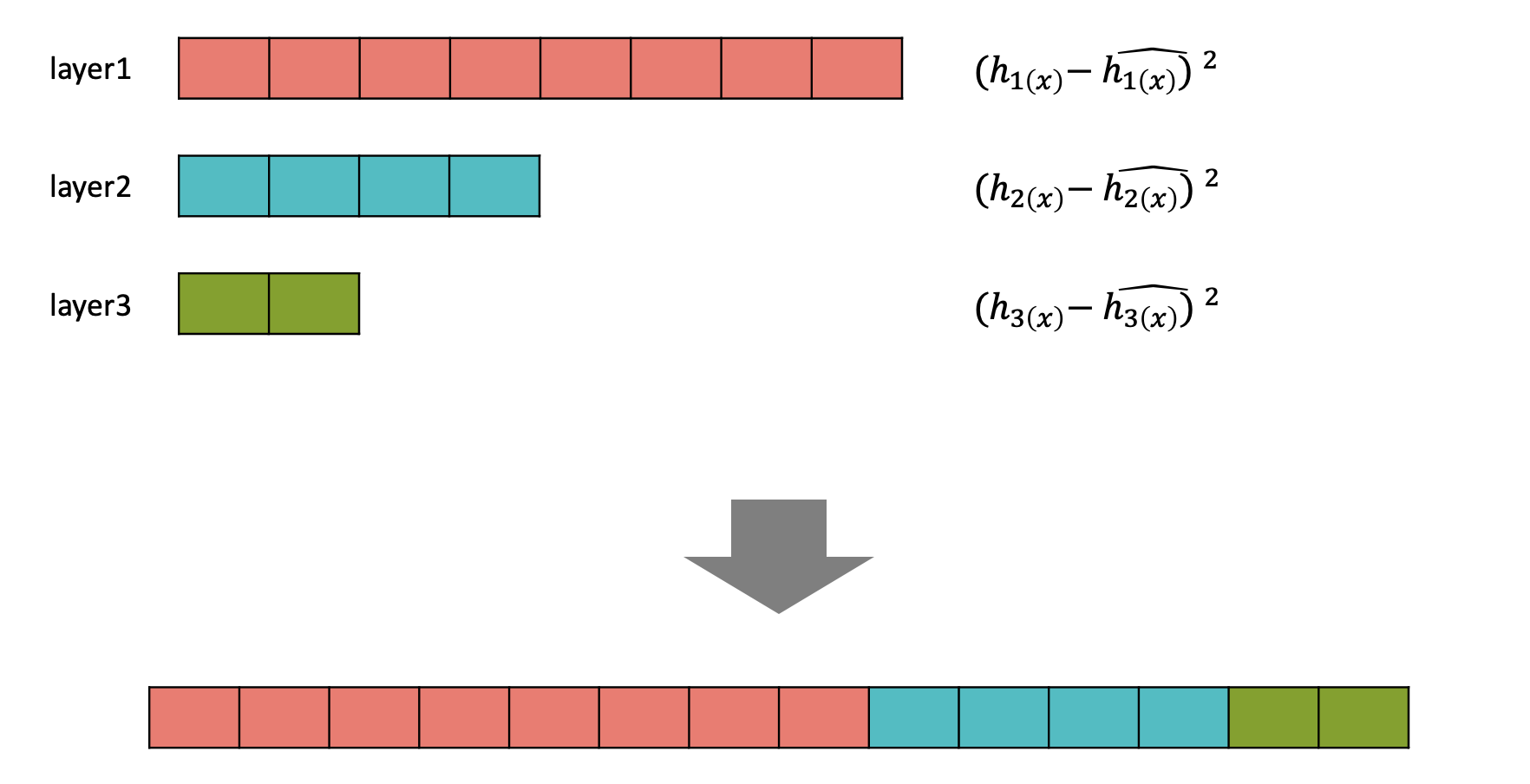
RaPP는 이렇게 concat한 값으로 Novelty(Abnormal) Score를 계산하는 방식에 SAP와 NAP 두 가지 방법을 소개한다.

 

SAP는 Simple Aggregation Along Pathway의 약자로, 모든 Enocder Layer의 \((h_n(x)\) - \(\hat{h_n(x)})^2\)를 concat 후 그냥 다 더해주면 된다. 즉, L2 Norm 혹은 MSE와 같은 아이디어이다. 

 

NAP는 Normalized Aggregation Along Pathway의 약자로, SAP를 Normalization 하는 개념으로, 마할라노비스 거리(Mahalanobis Distance)를 구하는 방식이다. 

 

마할라노비스 거리는 평균과의 거리가 표준편차의 몇 배인지를 나타내는 값이다.

예를 들어, 어떤 식당에 오는 사람 수가 하루 평균 20명, 표준편차가 3이라 하자. 

이 말은 하루에 평균적으로 오는 사람이 20명 정도인데, 항상 정확히 20명은 아니고, 17~23명 정도라는 뜻이다.

 

그럼 만약에 오늘은 26명이 방문했다 하자.

단순이 평균으로부터의 거리는 6명(=26-20)이다. 이를 마할라노비스 거리로 구하면 2(=(26-20)/3)가 된다.

즉, 표준편차의 2배정도 오차가 있는 값이라 해석할 수 있다.

 

https://darkpgmr.tistory.com/41

 

일반적으로 표준화(standardization) 할 때, \((x-\mu)/\sigma\) 하는 것과 같은 원리이다.

 

아래 코드를 보면, SVD(특이값 분해)를 하는데, 표준편차를 구하기 위해 하는 행위라고 이해하면 된다.

Train Set에 대한 평균과 표준편차를 구해서, Test Set에 적용하여 Normalization한다.

---

SAP와 NAP의 차이를 그림으로 보면 다음과 같다.

 

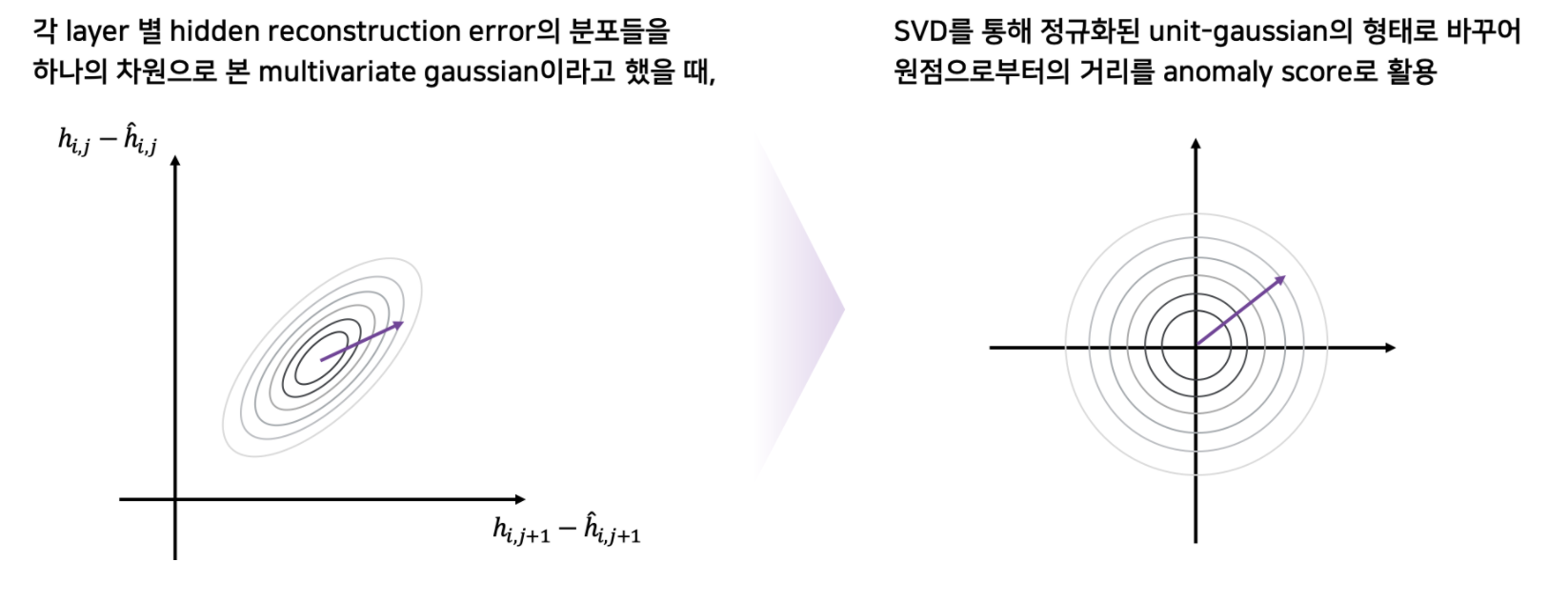
왼쪽 그림의 SAP는 각 layer에 대해 그냥 계산한 값이고, 오른쪽 그림의 NAP는 이를 normalization해서 계산한 값이다.

 

---

RaPP가 기존의 Reconstruction Error 방식보다 결과가 좋은 이유를 직관적으로 이해하자면,

일반적으로 Data들은 Noise를 가지고 있으며, 이 Noise가 적으면 Normal, 크면 Abnormal로  정의한다.

 

Auto Encoder 학습을 통해 Encoder 부분의 낮은 Dimension에서 다시 큰 Dimension으로 복원하는 과정에서 이 Noise들이 제거된다.

따라서 input data와 AE를 거쳐 나온 output을 비교하여 그 차이가 크다면, input data에 Noise가 많이 껴있다고 생각하여, Abnormal이라 판단한다(AE를 통해 나온 output은 Noise가 제거되었으므로). 이것이 기존의 Reconstruction Error로 Anomaly Detection을 하는 원리이다.

 

그렇다면, AE를 한 번 거치면 Abnormal data를 input으로 넣었다 하더라도, Noise가 제거되었으므로 어느정도 Normal data가 되었다고 할 수 있다.

즉, 이 Normal Data를 다시 AE 중 Encoder에 넣으면, 그 결과는 정상 데이터의 특징을 가지고 있을 것이다.

따라서, Encoder에 raw input을 넣었을 때의 결과와, AE를 한 번 거쳐서 정상 데이터가 된 input을 넣었을 때의 결과는 Normal Data에 비해 Abnormal Data의 차이가 더 클 것이다.

 

사실, 기존의 Reconsturction Error 구하는 이론과 기본적인 아이디어는 "Noise의 크기로 Abnormal을 판단한다는 점"에서 똑같다.

단, 하나의 Layer(input-output)만 가지고 계산하는 것보다, Encoder의 모든 Layer를 다 더해서 계산하는 것이 그 값을 더 극대화 시켜주는 원리이다.

 

---

이를 Tensorflow로 MNIST에 적용하는 코드를 짜보았다.

 

1. Import Library

 

from __future__ import division, print_function, absolute_import
 
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt 

import pandas as pd
import seaborn as sns

 

2. Loading Data

글쓴이는 아래 코드를 그냥 실행하면 에러가 나서, 주석 처리 해 놓은 코드도 함께 실행해 주었다.

 

# 아래 mnist loading 하는 부분 에러나면 실행

# import requests
# requests.packages.urllib3.disable_warnings()
# import ssl

# try:
#     _create_unverified_https_context = ssl._create_unverified_context
# except AttributeError:
#     # Legacy Python that doesn't verify HTTPS certificates by default
#     pass
# else:
#     # Handle target environment that doesn't support HTTPS verification
#     ssl._create_default_https_context = _create_unverified_https_context
    
# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)

 

데이터는 총 70,000건으로, 55,000건의 Train Set, 5,000건의 Validation Set, 10,000건의 Test Set으로 구성되어있으며, 28 by 28의 이미지가 784개의 컬럼으로 flatten 되어있다.

 

(Validation Set은 사용하지 않았다.)

 

---

2.1 Define Novelty

0~9의 총 10개의 class 중 1을 Novelty라 정의한다.

즉, 1을 뺀 총 9개의 class만 Train 시키고, 이후 1을 포함한 전체 class를 Test 하여, Novelty(=1)와 Normal(\(\ne\)1)의 Score를 비교한다. 

 

trainSet = mnist.train.images[np.argmax(mnist.train.labels==1, axis=1) != 1]
print("Dimension of Train Set : ", trainSet.shape)

 

> Dimension of Train Set : (48821, 784)

 

참고로 Train Set의 각 Label별 데이터 개수는 다음과 같다.

 

 

---

3. Set Parmameters

learning rate, batch size 등 parameter들을 설정한다.

모델 구조는 다음과 같다.

 

784(input) -> 256 -> 128 -> 64 -> 32 -> 64 -> 128 -> 256 -> 784(output) 

 

learning_rate = 0.01
num_steps = 10000
batch_size = 256
 
display_step = 1000
examples_to_show = 10
 
num_hidden_1 = 256
num_hidden_2 = 128
num_hidden_3 = 64
num_hidden_4 = 32
num_input = 784

 

---

4. Stacked AutoEncoder

이해하기 쉽게 짜기 위해 따로 function으로 묶거나, 구조화하지 않았다.

 

X = tf.placeholder("float", [None, num_input])

# Encoder
## 784 -> 256
w1 = tf.Variable(tf.random_normal([num_input, num_hidden_1]))
b1 = tf.Variable(tf.random_normal([num_hidden_1]))
h1 = tf.nn.sigmoid(tf.add(tf.matmul(X, w1), b1))

## 256 -> 126
w2 = tf.Variable(tf.random_normal([num_hidden_1, num_hidden_2]))
b2 = tf.Variable(tf.random_normal([num_hidden_2]))
h2 = tf.nn.sigmoid(tf.add(tf.matmul(h1, w2), b2))

## 126 -> 64
w3 = tf.Variable(tf.random_normal([num_hidden_2, num_hidden_3]))
b3 = tf.Variable(tf.random_normal([num_hidden_3]))
h3 = tf.nn.sigmoid(tf.add(tf.matmul(h2, w3), b3))

## 64 -> 32
w4 = tf.Variable(tf.random_normal([num_hidden_3, num_hidden_4]))
b4 = tf.Variable(tf.random_normal([num_hidden_4]))
h4 = tf.nn.sigmoid(tf.add(tf.matmul(h3, w4), b4))

# Decoder
## 32 -> 64
w5 = tf.Variable(tf.random_normal([num_hidden_4, num_hidden_3]))
b5 = tf.Variable(tf.random_normal([num_hidden_3]))
h5 = tf.nn.sigmoid(tf.add(tf.matmul(h4, w5), b5))

## 64 -> 126
w6 = tf.Variable(tf.random_normal([num_hidden_3, num_hidden_2]))
b6 = tf.Variable(tf.random_normal([num_hidden_2]))
h6 = tf.nn.sigmoid(tf.add(tf.matmul(h5, w6), b6))

## 126 -> 256
w7 = tf.Variable(tf.random_normal([num_hidden_2, num_hidden_1]))
b7 = tf.Variable(tf.random_normal([num_hidden_1]))
h7 = tf.nn.sigmoid(tf.add(tf.matmul(h6, w7), b7))

## 256 -> 784 : output
w8 = tf.Variable(tf.random_normal([num_hidden_1, num_input]))
b8 = tf.Variable(tf.random_normal([num_input]))
y_pred = tf.nn.sigmoid(tf.add(tf.matmul(h7, w8), b8))

 

---

5. Train & Test

loss와 optimizer까지 설정해주고, Train 한다.

 

# loss and optimizer
y_true = X

loss = tf.reduce_mean(tf.pow(y_true - y_pred, 2))
optimizer = tf.train.RMSPropOptimizer(learning_rate).minimize(loss)
 
init = tf.global_variables_initializer()

 

trainSet을 1을 빼고 새로 정의했기 때문에 mnist.train.next_batch()가 아니라 batch 개수 만큼 indexing해서 학습한다.

 

# with tf.Session() as sess:
sess = tf.Session() 
sess.run(init)

# Training
for i in range(1, num_steps+1):
#     batch_x, _ = mnist.train.next_batch(batch_size)

    if i%(trainSet.shape[0] // batch_size) == 0 :
        j = (trainSet.shape[0] // batch_size)
    else : j = i % (trainSet.shape[0] // batch_size)
        
    batch_x = trainSet[((j-1)*batch_size):(batch_size*j)]
    
    feed_dict_batch = {X : batch_x}
    _, l = sess.run([optimizer, loss], feed_dict=feed_dict_batch)
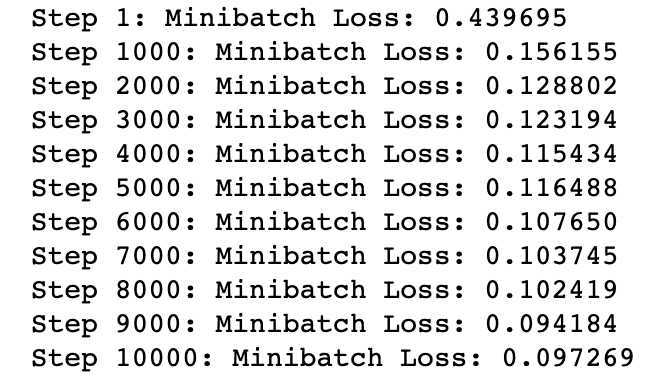
    if i % display_step == 0 or i == 1:
        print('Step %i: Minibatch Loss: %f' % (i, l))

 

---

모델이 잘 학습되었는지 확인하기 위해 input(X)과 output(y_pred)를 다시 28 by 28로 reshape하고 그림으로 그려 확인해보았다.

 

# Testing
n = 4
canvas_orig = np.empty((28 * n, 28 * n))
canvas_recon = np.empty((28 * n, 28 * n))
for i in range(n):
    batch_x, _ = mnist.test.next_batch(n)
    g = sess.run(y_pred, feed_dict={X: batch_x})

    for j in range(n):
        canvas_orig[i * 28:(i + 1) * 28, j * 28:(j + 1) * 28] = batch_x[j].reshape([28, 28])
    for j in range(n):
        canvas_recon[i * 28:(i + 1) * 28, j * 28:(j + 1) * 28] = g[j].reshape([28, 28])

print("Original Images")
plt.figure(figsize=(n, n))
plt.imshow(canvas_orig, origin="upper", cmap="gray")
plt.show()

print("Reconstructed Images")
plt.figure(figsize=(n, n))
plt.imshow(canvas_recon, origin="upper", cmap="gray")
plt.show()

 

 

epoch이 작아 깔끔하진 않지만, 나쁘지않다고 판단하여 이 모델로 Abnormal Score를 계산한다.

 

---

6. Calutation Reconstrunction Error

 

6.1 Original RE

RaPP가 아닌, 기존의 RE로 계산하면 다음과 같다.

test set을 input으로 넣고, prediction 한 후, input과 ouput의 차이를 계산한다.

Score는 그 차이를 제곱하고 더하여 마치 MSE 처럼 계산한다.

 

test_r = sess.run(y_pred, feed_dict={X:mnist.test.images})
re = ((mnist.test.images - test_r)**2).sum(axis=1)

 

Novelty(=1) 와 Normal(\(\ne\)1)의 RE 분포를 시각화하면 다음과 같다.

 

re_table = pd.DataFrame({'label':np.argmax(mnist.test.labels==1, axis=1),
                        're':re})
re_table['isOne'] = np.where(re_table['label']==1, "Novelty",'Normal')

label = ["Novelty",'Normal']
plt.figure(figsize = (18,5))
for a in label:
    subset = re_table[re_table['isOne'] == a]
    
    # Draw the density plot
    sns.distplot(subset['re'], hist = False, kde = True,
                 kde_kws = {'shade': True, 'linewidth': 3}, 
                  label = a)

plt.legend(prop={'size': 16}, title = 'label')

 

 

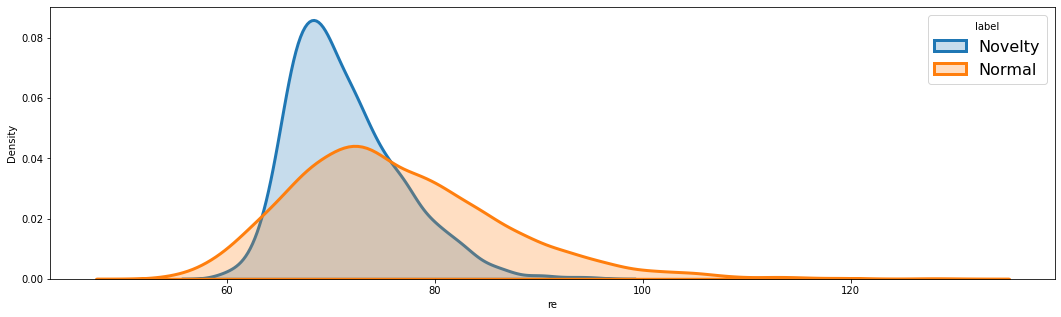
파란색이 Novelty, 주황색이 Normal에 대한 복원오차 분포이다.

한 번도 학습한 적 없는 Novelty 복원 오차의 분포가 Normal 복원 오차 분포 안에 속해있고, 오히려 값이 더 작다.

 

아마 1이라는 숫자가 너무 단순하게 생겨서 그런 듯 하다.

이러한 문제를 RaPP로 해결할 수 있다.

 

---

6.2 SAP

이번에는 RaPP 중 SAP를 계산해 보겠다.

 

먼저, Enocder에 대해 각 Layer별 raw input에 대한 값과 한 번 AE를 거친 input에 대한 값의 차이를 계산한다.

 

# h0
x_tilde = sess.run(y_pred, feed_dict={X:mnist.test.images}) 
sap0 = mnist.test.images - x_tilde # original reconstruction error

# h1 : prediction h1; h1(원래 데이터) - h1(x_tilde)
sap1 = sess.run(h1, feed_dict={X : mnist.test.images}) - sess.run(h1, feed_dict={X : x_tilde})

# h2
sap2 = sess.run(h2, feed_dict={X : mnist.test.images}) - sess.run(h2, feed_dict={X : x_tilde})

# h3
sap3 = sess.run(h3, feed_dict={X : mnist.test.images}) - sess.run(h3, feed_dict={X : x_tilde})

# h4
sap4 = sess.run(h4, feed_dict={X : mnist.test.images}) - sess.run(h4, feed_dict={X : x_tilde})

 

각 결과에 대한 Dimension은 다음과 같다.

test set이 10,000개 이므로, 모두 10,000개의 row로 이루어져있고,

input과 output을 비교한 sap0은 input dimension과 같은 784개의 컬럼,

첫 번째 encoder layer를 비교한 sap1는 256개의 컬럼을 가지고 있다.

 

---

이제 모든 encoder layer에 대한 차이값을 concat하고 score를 계산한다.

axis=1로 column-wise하게 concat한다.

 

sap = np.concatenate([sap1, sap2, sap3, sap4], axis =1)

 

concat 했을 때 컬럼의 수는 4개의 encoder 뉴런 수를 모두 더한 값과 같다.

480 = 256 + 128 + 64 + 32

 

 

이를 제곱해주고 더해주면 SAP Score가 된다.

 

sap = (sap**2).sum(axis=1)

 

---

마찬가지로 시각화하면 다음과 같다.

 

sap_table = pd.DataFrame({'label':np.argmax(mnist.test.labels==1, axis=1),
                        'sap':sap})
sap_table
sap_table = pd.DataFrame({'label':np.argmax(mnist.test.labels==1, axis=1),
                        'sap':sap})
sap_table['isOne'] = np.where(sap_table['label']==1, "Novelty",'Normal')

label = ["Novelty",'Normal']
plt.figure(figsize = (18,5))
for a in label:
    subset = sap_table[sap_table['isOne'] == a]
    
    # Draw the density plot
    sns.distplot(subset['sap'], hist = False, kde = True,
                 kde_kws = {'shade': True, 'linewidth': 3}, 
                  label = a)

plt.legend(prop={'size': 16}, title = 'label')

 

 

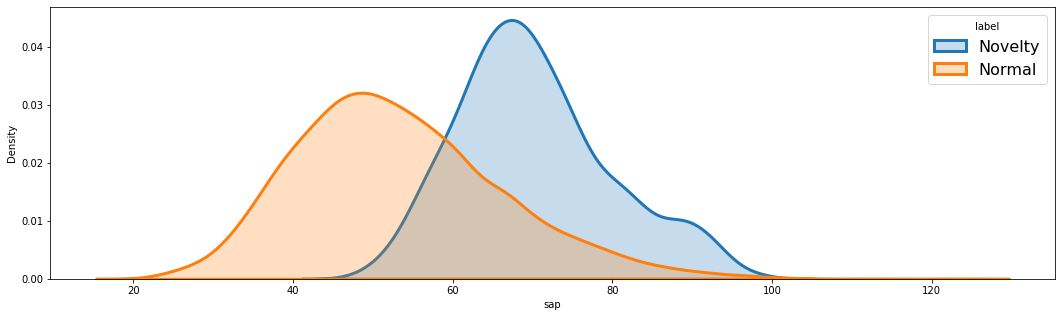
기존의 RE에 비해 Novelty와 Normal이 확실히 구분되고, Novelty의 Score가 커졌다.

 

---

6.3 NAP

이번에는 NAP를 계산해 보겠다.

NAP는 Train Set의 평균과 표준편차를 가지고 Normalization 하는 방법이므로, 

Train Set도 Encoder의 각 Layer에 대해 차이를 계산해준다.

 

# h0
x_tilde = sess.run(y_pred, feed_dict={X:trainSet})
train_nap0 = trainSet - x_tilde

# h1
train_nap1 = sess.run(h1, feed_dict={X : trainSet}) - sess.run(h1, feed_dict={X : x_tilde})

# h2
train_nap2 = sess.run(h2, feed_dict={X : trainSet}) - sess.run(h2, feed_dict={X : x_tilde})

# h3
train_nap3 = sess.run(h3, feed_dict={X : trainSet}) - sess.run(h3, feed_dict={X : x_tilde})

# h4
train_nap4 = sess.run(h4, feed_dict={X : trainSet}) - sess.run(h4, feed_dict={X : x_tilde})

 

train_nap = np.concatenate([train_nap1, train_nap2, train_nap3, train_nap4], axis =1)
test_nap = np.concatenate([sap1, sap2, sap3, sap4], axis =1)

 

Train Set의 표준편차를 구하기 위해 SVD(특이값 분해)한다. 

 

_, _, train_v = np.linalg.svd(train_nap - train_nap.mean(axis=0), full_matrices=False)

 

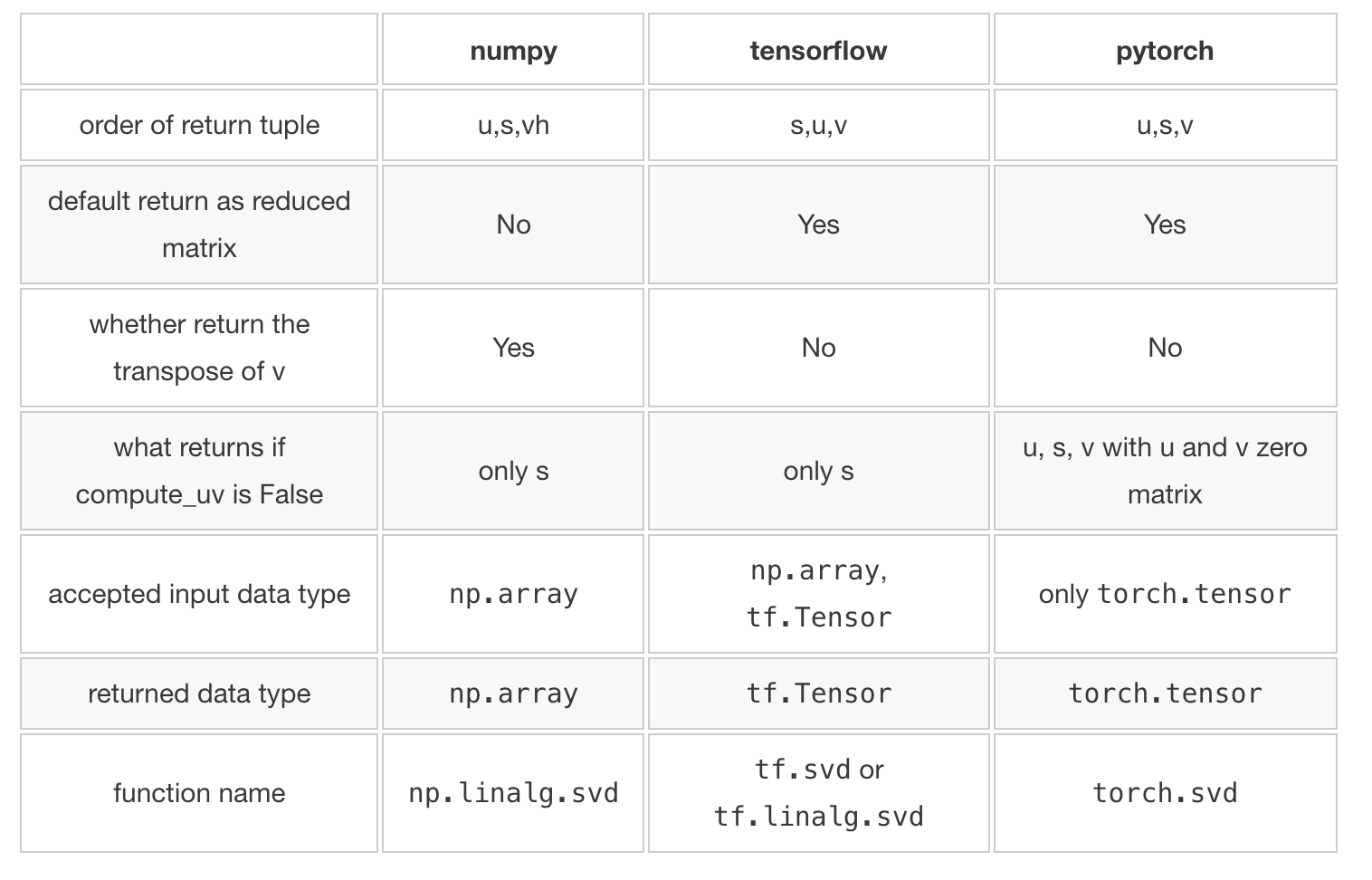
이 svd를 계산 과정에서 torch로 구현된 것과 다른 결과가 나와, 최종 Score도 값에 차이가 있다. (분포는 똑같으나, 값 자체에만 차이가 있는 것이므로 문제는 없다.)

 

3차원 공간에서 어떤 한 직선과 orthogonal한 직선을 찾는다고 생각해보면, 단 하나의 직선이 아니라 수많은 직선이 있을 것이다. 그래서 차이가 나는 것으로 보인다.

 

아래는 numpy, tensorflow, pytorch로 계산한 SVD에 대한 차이를 summary 해 놓은 표이다.

 

https://re-ra.xyz/Differences-of-SVD-methods-in-numpy,-tensorflow-and-pytorch/

 

이제 Train Set에 대한 분산(표준편차의 제곱)을 구하고, Test Set에 적용하여 NAP Score를 계산한다.

(평균과 분산은 각 컬럼별 평균과 분산이다. 즉, 아래 mean과 var은 480개의 값으로 이루어져있다.)

 

train_rotater = np.matmul(train_nap - train_nap.mean(axis=0), train_v.T)
test_rotater = np.matmul(test_nap - train_nap.mean(axis=0), train_v.T)

x = train_rotater - train_rotater.mean(axis=0)
var = np.cov(x.T).diagonal() #  train set 의 분산

nap = ((test_rotater-train_rotater.mean(axis=0))/(var**.5))
nap = (abs(nap)**2).mean(axis=1)

 

결과를 시각화하면 다음과 같다.

 

nap_table = pd.DataFrame({'label':np.argmax(mnist.test.labels==1, axis=1),
                        'nap':nap})
nap_table['isOne'] = np.where(nap_table['label']==1, "Novelty",'Normal')

label = ["Novelty",'Normal']
plt.figure(figsize = (18,5))
for a in label:
    subset = nap_table[nap_table['isOne'] == a]
    
    # Draw the density plot
    sns.distplot(subset['nap'], hist = False, kde = True,
                 kde_kws = {'shade': True, 'linewidth': 3}, 
                  label = a)

plt.legend(prop={'size': 16}, title = 'label')

 

 

앞 부분만 확대하면 다음과 같다.

 

 

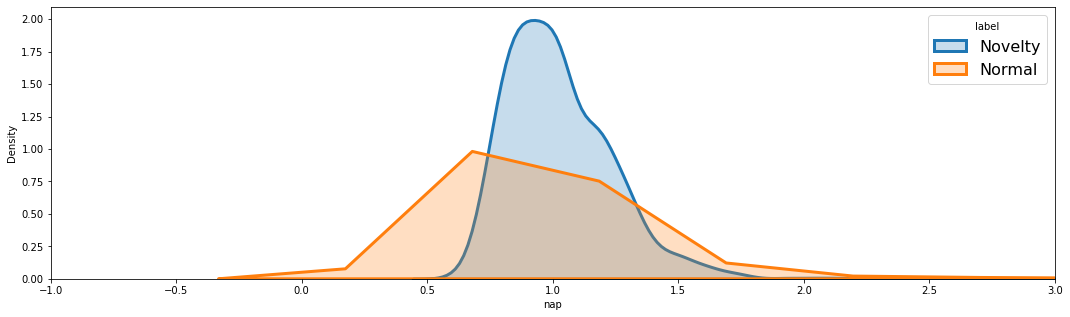
SAP 만큼은 아니지만, Novelty 의 Score가 조금은 커졌다.

 

---

논문의 저자가 제공한 코드에서는 각각 10개의 layer로 구성된 encoder와 decoder로 AE를 쌓았으며, Activation function도 글쓴이는 sigmoid를 사용하였고, 논문의 저자는 LeakyRelu를 사용하는 등 Model Structure에 차이가 있다.

이러한 이유로 논문 저자가 제시한 결과와 글쓴이의 결과에 차이가 있는 듯 하다.

 

논문 저자의 결과

 

---

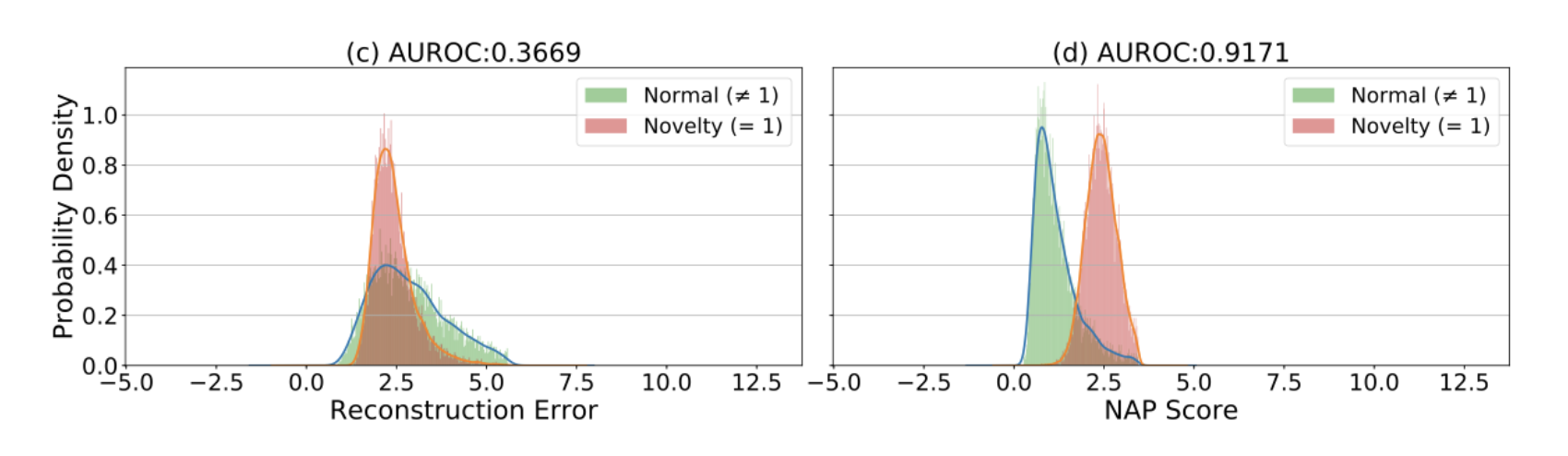
이 논문의 저자는 아래와 같이 encoder layer만 비교하는 것이 아니라, encoder와 decoder를 함께 비교하는 방법도 시도해 보았다.

 

 

 

하지만, 이 방법은 효과가 없었다고 한다.

AE는 학습 과정에서 단지 입력과 출력이 같아지기만을 신경 쓸 뿐, 중간 layer들은 신경쓰지 않는다. 즉, 논문의 저자가 표현하기를 "모로 가든 서울로만 가면 된다"고 중간 레이어에서 어떤 값이 나왔던간에, 디코더의 최종 출력값이 입력값과 비슷하기만 하면 된다.

중간 결과값에 대한 어떠한 제약도 없기 때문에, 중간 결과값끼리의 비교는 무의미하다.

 

 

---

후기

처음에 각 layer를 4개씩이 아니라 2개씩 쌓았을 때는 결과가 그닥 좋지 않았다. 생각해보면 당연하다.

RaPP가 기존의 RE 보다 좋은 이유는 위에도 있지만, 하나의 layer만 비교하던 기존 방식에 비해 여러개의 layer를 더하므로써 그 차이를 극대화 하는 것인데, layer 수가 작으면 당연히 효과가 작아질 것이다.

 

즉, layer를 많이 쌓을 수록 효과가 극명하다는 것이고, 이는 layer가 깊은 복잡한 모델에서도 잘 작동할 수 있도록 양질의 데이터가 많아야 한다는 뜻이다.