이전 포스팅에서 Genetic Algorithm의 원리와 R에서 GA 라이브러리 사용법에 대해 알아보았다.
[Optimization] 최적화 알고리즘 :: GA(Genetic Algorithm, 유전 알고리즘)란? GA 예시, R로 GA 구현하기
제조 공정에서 최적화란? 딥러닝을 공부한 사람이라면 최적화(Optimization)이라는 단어를 많이 들어보았을 것이다. 딥러닝에서 모델을 학습하는 과정에서 Cost function 값을 최소화 시키기 위한 Weight
leedakyeong.tistory.com
[R] GA 특정 값으로 최적화 하는 방법 (no Maximizing) :: How to optimize with GA specific values in R
R에서 GA 최대값으로 최적화 하지 않고, 지정된 값으로 최적화 하는 방법 Genetic Algorithm(GA - 유전 알고리즘) 최적화 문제를 해결하는 기법 중 하나로, 생물의 진화를 모방한 방법이다. R에서는 GA 패
leedakyeong.tistory.com
이번에는 최적화 하고 싶은 function이 여러개 일 때, 즉 Multi Objective Optimization에 대해 알아보겠다.
Multi Objective Optimization with GA 원리
GA에서 최적화하고자 하는 function이 여러개 일때, 최적값을 찾는 원리를 설명하겠다.
여기를 참고하였다.
Objective function이 한 개 일 때는 기본으로 주어진 function을 Maximization하는 것이 목적이었다.
그러나 최적화 하고자 하는 function이 여러개 일 때는 대부분의 오픈 소스들이 Minimization을 목적으로 한다.
Multi-Objective Optimization Problem(MOOP)에서도 GA의 기본 원리는 One-Objective Optimization Problem에서의 GA와 같다.
초기 염색체들을 생성하고 -> 주어진 function에 fitting해서 적합도 기반으로 Selection하고 -> Crossover -> Mutation -> ... 반복의 과정이다.
단, 차이점은 더 좋은 염색체를 선택할 때 Pareto Front 기반으로 선택을 하게된다.
Pareto란 한정된 자원이 효율적으로 배분된 상태를 말한다. 즉, 하나의 자원배분 상태에서 다른 사람에게 손해가 가도록 하지 않고서는 어떤 한 사람에게 이득이 되는 변화를 만들어내는 것이 불가능할 때 이 배분 상태를 ‘파레토 효율적’이라고 한다.
Pareto Front
MOOP에는 둘 이상의 목적 함수가 있기 때문에, 솔루션A가 솔루션B보다 더 낫다고 직관적으로 이해하기가 어렵다.
따라서 다음과 같을 때 솔루션A가 B보다 더 좋다고 정의한다.
Given
- A vector of objective function $\vec{f}(\vec{x}) = [f_1(\vec{x}), f_2(\vec{x}), ..., f_k(\vec{x})] $
- And a feasible solution of Ω
In a minimization problem, a vector $\vec{x}$ better than $\vec{y}$ if:
- $f_i\vec{x} \le f_i\vec{y}$ for all $i$ function in $f_i$
- There is at least one $i$ such that $f_i\vec{x} < f_i\vec{y}$
즉, 모든 f(x) 가 모든 f(y)에 대해 값이 더 작거나 같고, 단 하나의 f(x)만 f(y)보다 작은것이 있으면 솔루션x를 솔루션y보다 좋다고 한다.
(x가 y보다 더 좋다는 것을 x가 y를 dominate한다고 표현한다.)
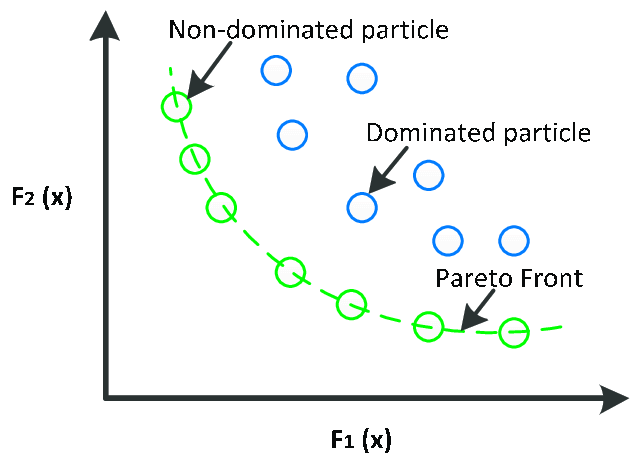
다음 그림을 보자.

X축이 첫 번째 Objective function(f1), Y축이 두 번째 Objective function(f2)으로, 이 두 function을 최소화 하는 솔루션을 찾는 것이 목표라 하자. 현재 찾은 해는 A, B, C, D가 있다.
두 함수를 모두 최소화 하는 것이 목적이므로, 그래프에서 왼쪽 아래에 가까운 해가 가장 좋은 Solution이 된다.
- SolutionB는 A에 비해 f2값은 작지만 f1값이 더 크므로 더 좋다고도, 나쁘다고도 말할 수 없다.
- A역시 비슷하게 B보다 더 좋지도, 나쁘지도 않다.(A와 B는 서로 dominate하지 않다 = non-dominated) 그러므로 두 해를 같은 Group으로 묶는다. :: Front 1
- SolutionC는 B보다 f1, f2 모두 값이 크고 A보다 f1값은 같고, f2값은 크다. 그러므로 A, B보다 좋지 않다.(C는 A와 B에 dominate하다. = C is dominated by solution A and B) :: Front 2
- SolutionD는 A, B, C보다 모두 나쁘다.(D is dominated by A,B, and C) :: Front 3
따라서 SolutionA와 B가 Pareto Front가 된다.
MOOP의 경우 GA 알고리즘에서 더 좋은 염색체를 선택할 때마다 이 Pareto Front를 선택한다.
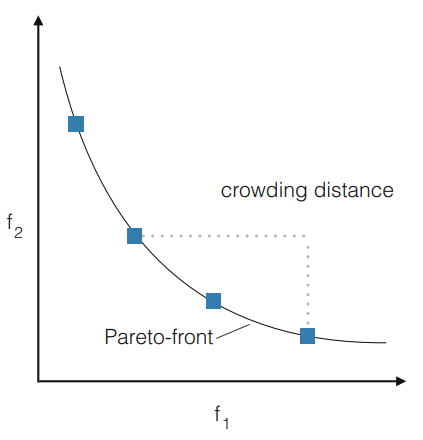
단, 다양성을 위해 같은 Pareto Front 중에서도 거리(Manhattan distance)가 먼 솔루션들을 선택한다.
거리가 가까이 있는 솔루션일 수록 비슷한 결과를 내기 때문이다.
Multi Objective Optimization with GA in R
R에서 GA로 MOOP을 해결하는 방법은 mco 라이브러리에 nsga2()에 구현되어 있다.
이해를 돕기 위해 단순한 예시로 설명하겠다.
3차원이 넘어가면 시각화가 어려워지므로, 찾고자 하는 최적값은 1개, 목적 함수는 2개로 한다.
목적함수는 다음과 같이 정의한다.
f1 <- function(x) -((x^2+x)*cos(x))
f2 <- function(x) x**2

왼쪽이 f1, 오른쪽이 f2에대한 시각화 그래프이다. x의 범위는 -10~10으로 제한하였다.
f1을 최소화 시키기위한 x는 6~7정도의 값이며, f2를 최소화시키기위한 x값은 0이다.
이렇게 상충되는 두 objective function을 모두 최소화시키기 위한 x를 GA로 찾아보겠다.
fun <- function(x) {
y <- numeric(2)
y[1] <- f1(x)
y[2] <- f2(x)
return (y)
}
opti <- nsga2(fn = fun,
idim = 1,
odim = 2,
generations=150,
popsize=100,
lower.bounds=-10,
upper.bounds=10)
nsga2의 parameter는 다음과 같다.
- fn : Fitness function
- idim : Number of decision values
- odim : Number of objective functions
그 외에 parameter들은 기존의 GA와 동일하다.
주어진 x를 두 목적함수에 적합시키는 function을 정의하여 fn에 파라미터로 입력해준다.
x의 범위도 lower.bounds와 upper.bounds로 입력한다.
x가 여러개일 때는 여기에도 x의 개수만큼 입력해주어야한다.(ex lower.bounds = c(-10, -10))
GA의 결과가 담긴 opti는 다음과 같다.

par에 최적의 x들이 100개(popSize)만큼 있고,
value에는 par를 적합시킨 f1, f2값들이 있다.
이를 하나의 data frame으로 만들면 다음과 같다.
temp <- bind_cols(x = opti$par,
y1 = opti$value[,1],
y2 = opti$value[,2]) %>% as.data.frame()

nsga2가 찾은 해를 시각화해보면 다음과 같다.
빨간색 vertical line이 nsga2가 찾은 해이다.
par(mfrow=c(2,1))
curve(f1, -10, 10)
abline(v=opti$par, col="#F8766D", lty = "dashed")
curve(f2, -10, 10)
abline(v=opti$par, col="#F8766D", lty = "dashed")

이 문제에서 f1과 f2를 모두 최소화 시킬수 있는 x는 없다.
결과를 보니 f2보다는 f1 최소화에 더 집중된 듯 하다.
찾은 x들의 분포는 다음과 같다.

5와 6사이의 값이 많이 찾아졌다.
본 포스팅에서는 쉬운 이해를 위해 간단한 문제를 예로 들었으나,
실제로는 Objective function이 3개 이상도 가능하고, x 역시 2개, 3개 이상도 가능하다.
mco에 nsga2외에도 nsga2R라이브러리에도 같은 기능이 구현되어있다.
python에서도 역시 MOOP을 해결하기위한 여러 오픈소스들이 있는데,
여기가면 각 패키지별로 몇 개의 objective function을 지원하는지, 어떤 알고리즘 기반인지 등 잘 정리되어있다.