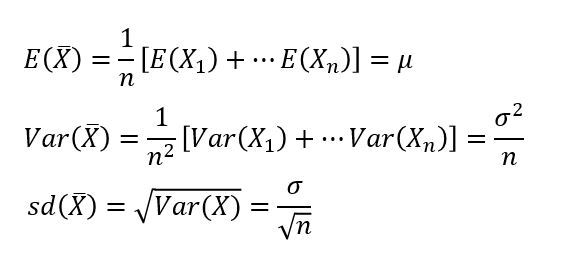표본평균의 분포 모평균에 대한 추론은 표본의 평균 X̄와 그 분포를 이용한다.평균이 μ이고 분산이 σ^2인 모집단으로부터 크기가 n인 표본 X1, X2, ..., Xn을 추출했을 때, 표본평균 X̄의 기댓값과 분산은 다음과 같다. 표본평균 분포의 중심은 모집단의 중심 μ와 일치한다. 그러나 표집분포의 퍼짐 정도를 측정하는 표준편차는 표본의 크기에도 영향을 받는다. 즉, 표본의 크기 n이 증가함에 따라 표본평균의 표준편차는 n의 제곱근에 반비례해서 감소하는데 이는 표본평균의 분포가 μ를 중심으로 더욱 집중됨을 나타낸다. 예를 들어, 표본의 크기를 100배 늘리면, 표본평균의 표준편차는 1/10으로 감소하여 표집분포가 μ를 중심으로 더욱 집중된다. 중심극한정리란? 모집단의 분포가 정규분포가 아닌 경우 X̄의..